7. Inject a known signal into a FrequencySeries¶

It can often be useful to add some known signal to inherently random or noisy data. For example, one might want to investigate what would happen if a binary black hole merger signal occured at or near the time of a glitch. In LIGO data analysis, this procedure is referred to as an _injection_.

In the example below we will create a stream of random, white Gaussian noise, then inject a loud, steady sinuosoid. We will do this in the frequency domain because it is much easier to model a sinusoid there.

First, we prepare one second of Gaussian noise:

from numpy import random
from gwpy.timeseries import TimeSeries
noise = TimeSeries(random.normal(scale=.1, size=1024), sample_rate=1024)

To inject a signal in the frequency domain, we need to take an FFT:

noisefd = noise.fft()

We can now easily inject a loud sinusoid of unit amplitude at, say, 30 Hz. To do this, we use inject().

import numpy
from gwpy.frequencyseries import FrequencySeries
signal = FrequencySeries(numpy.array([1.]), f0=30, df=noisefd.df)
injfd = noisefd.inject(signal)

We can then visualize the data before and after injection in the frequency domain:

from gwpy.plot import Plot
plot = Plot(numpy.abs(noisefd), numpy.abs(injfd), separate=True,
            sharex=True, sharey=True, xscale='log', yscale='log')
plot.show()

(png)

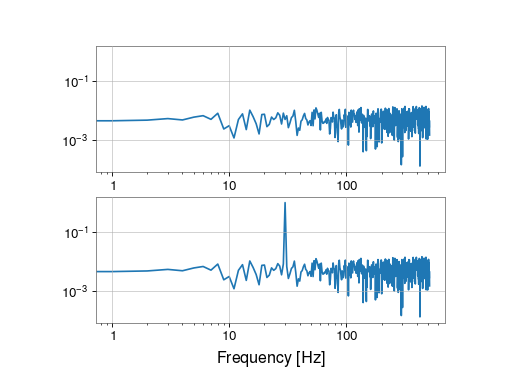
Finally, for completeness we can visualize the effect before and after injection back in the time domain:

inj = injfd.ifft()
plot = Plot(noise, inj, separate=True, sharex=True, sharey=True,
            figsize=(12, 6))
plot.show()

(png)

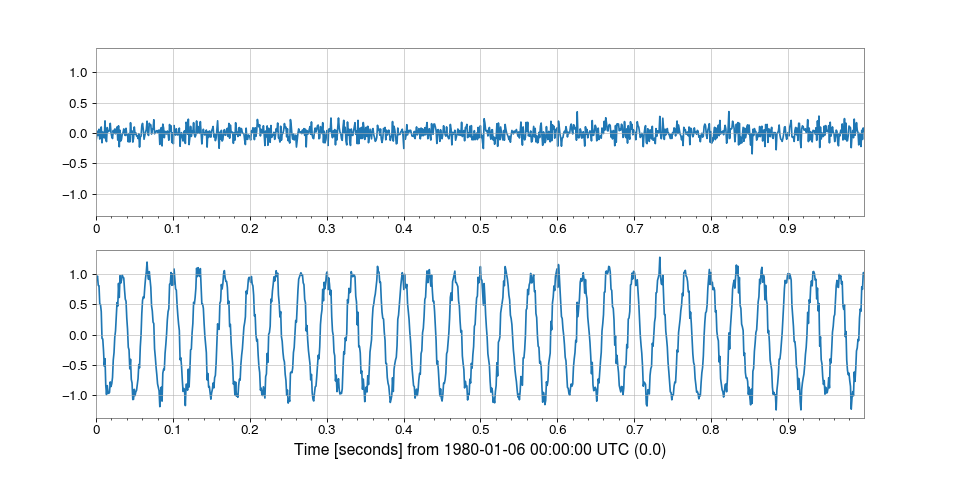
We can see why sinusoids are easier to inject in the frequency domain: they only require adding at a single frequency.