2. Plotting a normalised Spectrogram¶

The previous example showed how to generate and display a Spectrogram of the LIGO-Hanford strain data around the GW150914 event.

However, because of the shape of the LIGO sensitivity curve, picking out features in the most sensitive frequency band (a few hundred Hertz) is very hard.

We can normalise our Spectrogram to highligh those features.

Again, we import the TimeSeries and call TimeSeries.fetch_open_data() the download the strain data for the LIGO-Hanford interferometer

from gwpy.timeseries import TimeSeries
data = TimeSeries.fetch_open_data(
    'H1', 'Sep 14 2015 09:45', 'Sep 14 2015 09:55')

Next, we can calculate a Spectrogram using the spectrogram() method of the TimeSeries over a 2-second stride with a 1-second FFT and # .5-second overlap (50%):

specgram = data.spectrogram(2, fftlength=1, overlap=.5) ** (1/2.)

and can normalise it against the overall median ASD by calling the ratio() method:

normalised = specgram.ratio('median')

Finally, we can make a plot using the plot() method

plot = normalised.plot(norm='log', vmin=.1, vmax=10, cmap='Spectral_r')
ax = plot.gca()
ax.set_yscale('log')
ax.set_ylim(10, 2000)
ax.colorbar(label='Relative amplitude')
plot.show()

(png)

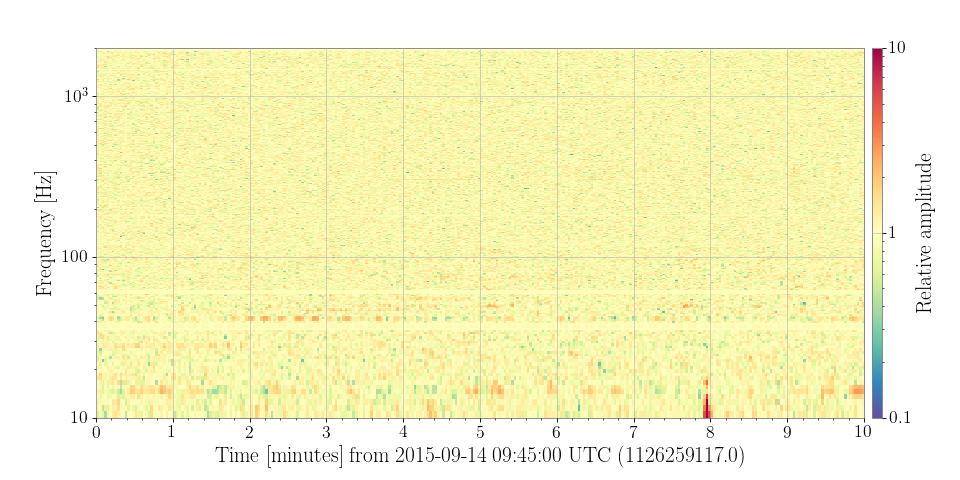
Even with a normalised spectrogram, the resolution is such that a signal as short as that of GW150914 is impossible to see. The next example uses a high-resolution spectrogram method to zoom in around the exact time of the signal.