TimeSeries¶

class gwpy.timeseries.TimeSeries[source]¶

Bases: gwpy.timeseries.core.TimeSeriesBase

A time-domain data array.

Parameters

value : array-like

input data array

unit : Unit, optional

physical unit of these data

t0 : LIGOTimeGPS, float, str, optional

GPS epoch associated with these data, any input parsable by to_gps is fine

dt : float, Quantity, optional

time between successive samples (seconds), can also be given inversely via sample_rate

sample_rate : float, Quantity, optional

the rate of samples per second (Hertz), can also be given inversely via dt

times : array-like

the complete array of GPS times accompanying the data for this series. This argument takes precedence over t0 and dt so should be given in place of these if relevant, not alongside

name : str, optional

descriptive title for this array

channel : Channel, str, optional

source data stream for these data

dtype : dtype, optional

input data type

copy : bool, optional

choose to copy the input data to new memory

subok : bool, optional

allow passing of sub-classes by the array generator

Notes

The necessary metadata to reconstruct timing information are recorded in the epoch and sample_rate attributes. This time-stamps can be returned via the times property.

All comparison operations performed on a TimeSeries will return a StateTimeSeries - a boolean array with metadata copied from the starting TimeSeries.

Examples

>>> from gwpy.timeseries import TimeSeries

To create an array of random numbers, sampled at 100 Hz, in units of ‘metres’:

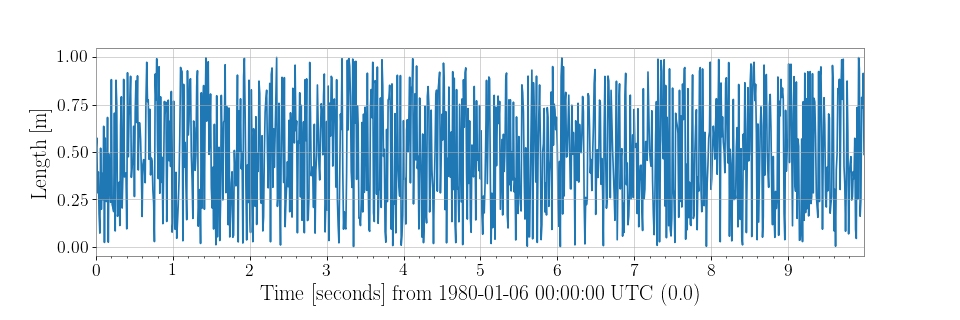
>>> from numpy import random
>>> series = TimeSeries(random.random(1000), sample_rate=100, unit='m')

which can then be simply visualised via

>>> plot = series.plot()
>>> plot.show()

(png)

Attributes Summary

T	The transposed array.
base	Base object if memory is from some other object.
cgs	Returns a copy of the current Quantity instance with CGS units.
channel	Instrumental channel associated with these data
ctypes	An object to simplify the interaction of the array with the ctypes module.
data	Python buffer object pointing to the start of the array’s data.
dt	X-axis sample separation
dtype	Data-type of the array’s elements.
duration	Duration of this series in seconds
dx	X-axis sample separation
epoch	GPS epoch for these data.
equivalencies	A list of equivalencies that will be applied by default during unit conversions.
flags	Information about the memory layout of the array.
flat	A 1-D iterator over the Quantity array.
imag	The imaginary part of the array.
info([option, out])	Container for meta information like name, description, format.
isscalar	True if the value of this quantity is a scalar, or False if it is an array-like object.
itemsize	Length of one array element in bytes.
name	Name for this data set
nbytes	Total bytes consumed by the elements of the array.
ndim	Number of array dimensions.
real	The real part of the array.
sample_rate	Data rate for this TimeSeries in samples per second (Hertz).
shape	Tuple of array dimensions.
si	Returns a copy of the current Quantity instance with SI units.
size	Number of elements in the array.
span	X-axis [low, high) segment encompassed by these data
strides	Tuple of bytes to step in each dimension when traversing an array.
t0	X-axis coordinate of the first data point
times	Positions of the data on the x-axis
unit	The physical unit of these data
value	The numerical value of this instance.
x0	X-axis coordinate of the first data point
xindex	Positions of the data on the x-axis
xspan	X-axis [low, high) segment encompassed by these data
xunit	Unit of x-axis index

Methods Summary

abs(x, /[, out, where, casting, order, …])	Calculate the absolute value element-wise.
all([axis, out, keepdims])	Returns True if all elements evaluate to True.
any([axis, out, keepdims])	Returns True if any of the elements of a evaluate to True.
append(self, other[, inplace, pad, gap, resize])	Connect another series onto the end of the current one.
argmax([axis, out])	Return indices of the maximum values along the given axis.
argmin([axis, out])	Return indices of the minimum values along the given axis of a.
argpartition(kth[, axis, kind, order])	Returns the indices that would partition this array.
argsort([axis, kind, order])	Returns the indices that would sort this array.
asd(self[, fftlength, overlap, window, method])	Calculate the ASD FrequencySeries of this TimeSeries
astype(dtype[, order, casting, subok, copy])	Copy of the array, cast to a specified type.
auto_coherence(self, dt[, fftlength, …])	Calculate the frequency-coherence between this TimeSeries and a time-shifted copy of itself.
average_fft(self[, fftlength, overlap, window])	Compute the averaged one-dimensional DFT of this TimeSeries.
bandpass(self, flow, fhigh[, gpass, gstop, …])	Filter this TimeSeries with a band-pass filter.
byteswap([inplace])	Swap the bytes of the array elements
choose(choices[, out, mode])	Use an index array to construct a new array from a set of choices.
clip([min, max, out])	Return an array whose values are limited to [min, max].
coherence(self, other[, fftlength, overlap, …])	Calculate the frequency-coherence between this TimeSeries and another.
coherence_spectrogram(self, other, stride[, …])	Calculate the coherence spectrogram between this TimeSeries and other.
compress(condition[, axis, out])	Return selected slices of this array along given axis.
conj()	Complex-conjugate all elements.
conjugate()	Return the complex conjugate, element-wise.
convolve(self, fir[, window])	Convolve this TimeSeries with an FIR filter using the
copy([order])	Return a copy of the array.
correlate(self, mfilter[, window, detrend, …])	Cross-correlate this TimeSeries with another signal
crop(self[, start, end, copy])	Crop this series to the given x-axis extent.
csd(self, other[, fftlength, overlap, window])	Calculate the CSD FrequencySeries for two TimeSeries
csd_spectrogram(self, other, stride[, …])	Calculate the cross spectral density spectrogram of this
cumprod([axis, dtype, out])	Return the cumulative product of the elements along the given axis.
cumsum([axis, dtype, out])	Return the cumulative sum of the elements along the given axis.
decompose(self[, bases])	Generates a new Quantity with the units decomposed.
demodulate(self, f[, stride, exp, deg])	Compute the average magnitude and phase of this TimeSeries once per stride at a given frequency
detrend(self[, detrend])	Remove the trend from this TimeSeries
diagonal([offset, axis1, axis2])	Return specified diagonals.
diff(self[, n, axis])	Calculate the n-th order discrete difference along given axis.
dot(b[, out])	Dot product of two arrays.
dump(file)	Dump a pickle of the array to the specified file.
dumps()	Returns the pickle of the array as a string.
ediff1d(self[, to_end, to_begin])
fetch(channel, start, end[, host, port, …])	Fetch data from NDS
fetch_open_data(ifo, start, end[, …])	Fetch open-access data from the LIGO Open Science Center
fft(self[, nfft])	Compute the one-dimensional discrete Fourier transform of this TimeSeries.
fftgram(self, fftlength[, overlap, window])	Calculate the Fourier-gram of this TimeSeries.
fill(value)	Fill the array with a scalar value.
filter(self, \*filt, \*\*kwargs)	Filter this TimeSeries with an IIR or FIR filter
find(channel, start, end[, frametype, pad, …])	Find and read data from frames for a channel
flatten(self[, order])	Return a copy of the array collapsed into one dimension.
from_lal(lalts[, copy])	Generate a new TimeSeries from a LAL TimeSeries of any type.
from_nds2_buffer(buffer_[, scaled, copy])	Construct a new series from an nds2.buffer object
from_pycbc(pycbcseries[, copy])	Convert a pycbc.types.timeseries.TimeSeries into a TimeSeries
gate(self[, tzero, tpad, whiten, threshold, …])	Removes high amplitude peaks from data using inverse Planck window.
get(channel, start, end[, pad, scaled, …])	Get data for this channel from frames or NDS
getfield(dtype[, offset])	Returns a field of the given array as a certain type.
heterodyne(self, phase[, stride, singlesided])	Compute the average magnitude and phase of this TimeSeries once per stride after heterodyning with a given phase series
highpass(self, frequency[, gpass, gstop, …])	Filter this TimeSeries with a high-pass filter.
inject(self, other)	Add two compatible Series along their shared x-axis values.
insert(self, obj, values[, axis])	Insert values along the given axis before the given indices and return a new Quantity object.
is_compatible(self, other)	Check whether this series and other have compatible metadata
is_contiguous(self, other[, tol])	Check whether other is contiguous with self.
item(*args)	Copy an element of an array to a standard Python scalar and return it.
itemset(*args)	Insert scalar into an array (scalar is cast to array’s dtype, if possible)
lowpass(self, frequency[, gpass, gstop, …])	Filter this TimeSeries with a Butterworth low-pass filter.
max([axis, out, keepdims, initial, where])	Return the maximum along a given axis.
mean([axis, dtype, out, keepdims])	Returns the average of the array elements along given axis.
median(self[, axis])	Compute the median along the specified axis.
min([axis, out, keepdims, initial, where])	Return the minimum along a given axis.
nansum(self[, axis, out, keepdims])
newbyteorder([new_order])	Return the array with the same data viewed with a different byte order.
nonzero()	Return the indices of the elements that are non-zero.
notch(self, frequency[, type, filtfilt])	Notch out a frequency in this TimeSeries.
override_unit(self, unit[, parse_strict])	Forcefully reset the unit of these data
pad(self, pad_width, \*\*kwargs)	Pad this series to a new size
partition(kth[, axis, kind, order])	Rearranges the elements in the array in such a way that the value of the element in kth position is in the position it would be in a sorted array.
plot(self[, method, figsize, xscale])	Plot the data for this timeseries
prepend(self, other[, inplace, pad, gap, resize])	Connect another series onto the start of the current one.
prod([axis, dtype, out, keepdims, initial, …])	Return the product of the array elements over the given axis
psd(self[, fftlength, overlap, window, method])	Calculate the PSD FrequencySeries for this TimeSeries
ptp([axis, out, keepdims])	Peak to peak (maximum - minimum) value along a given axis.
put(indices, values[, mode])	Set a.flat[n] = values[n] for all n in indices.
q_gram(self[, qrange, frange, mismatch, …])	Scan a TimeSeries using the multi-Q transform and return an EventTable of the most significant tiles
q_transform(self[, qrange, frange, gps, …])	Scan a TimeSeries using the multi-Q transform and return an interpolated high-resolution spectrogram
ravel([order])	Return a flattened array.
rayleigh_spectrogram(self, stride[, …])	Calculate the Rayleigh statistic spectrogram of this TimeSeries
rayleigh_spectrum(self[, fftlength, overlap])	Calculate the Rayleigh FrequencySeries for this TimeSeries.
read(source, \*args, \*\*kwargs)	Read data into a TimeSeries
repeat(repeats[, axis])	Repeat elements of an array.
resample(self, rate[, window, ftype, n])	Resample this Series to a new rate
reshape(shape[, order])	Returns an array containing the same data with a new shape.
resize(new_shape[, refcheck])	Change shape and size of array in-place.
rms(self[, stride])	Calculate the root-mean-square value of this TimeSeries once per stride.
round([decimals, out])	Return a with each element rounded to the given number of decimals.
searchsorted(v[, side, sorter])	Find indices where elements of v should be inserted in a to maintain order.
setfield(val, dtype[, offset])	Put a value into a specified place in a field defined by a data-type.
setflags([write, align, uic])	Set array flags WRITEABLE, ALIGNED, (WRITEBACKIFCOPY and UPDATEIFCOPY), respectively.
shift(self, delta)	Shift this Series forward on the X-axis by delta
sort([axis, kind, order])	Sort an array in-place.
spectral_variance(self, stride[, fftlength, …])	Calculate the SpectralVariance of this TimeSeries.
spectrogram(self, stride[, fftlength, …])	Calculate the average power spectrogram of this TimeSeries using the specified average spectrum method.
spectrogram2(self, fftlength[, overlap, window])	Calculate the non-averaged power Spectrogram of this TimeSeries
squeeze([axis])	Remove single-dimensional entries from the shape of a.
std([axis, dtype, out, ddof, keepdims])	Returns the standard deviation of the array elements along given axis.
step(self, \*\*kwargs)	Create a step plot of this series
sum([axis, dtype, out, keepdims, initial, where])	Return the sum of the array elements over the given axis.
swapaxes(axis1, axis2)	Return a view of the array with axis1 and axis2 interchanged.
take(indices[, axis, out, mode])	Return an array formed from the elements of a at the given indices.
taper(self[, side, duration, nsamples])	Taper the ends of this TimeSeries smoothly to zero.
to(self, unit[, equivalencies])	Return a new Quantity object with the specified unit.
to_lal(self)	Convert this TimeSeries into a LAL TimeSeries.
to_pycbc(self[, copy])	Convert this TimeSeries into a PyCBC TimeSeries
to_string(self[, unit, precision, format, …])	Generate a string representation of the quantity and its unit.
to_value(self[, unit, equivalencies])	The numerical value, possibly in a different unit.
tobytes([order])	Construct Python bytes containing the raw data bytes in the array.
tofile(fid[, sep, format])	Write array to a file as text or binary (default).
tolist()	Return the array as an a.ndim-levels deep nested list of Python scalars.
tostring([order])	Construct Python bytes containing the raw data bytes in the array.
trace([offset, axis1, axis2, dtype, out])	Return the sum along diagonals of the array.
transpose(*axes)	Returns a view of the array with axes transposed.
update(self, other[, inplace])	Update this series by appending new data from an other and dropping the same amount of data off the start.
value_at(self, x)	Return the value of this Series at the given xindex value
var([axis, dtype, out, ddof, keepdims])	Returns the variance of the array elements, along given axis.
view([dtype, type])	New view of array with the same data.
whiten(self[, fftlength, overlap, method, …])	Whiten this TimeSeries using inverse spectrum truncation
write(self, target, \*args, \*\*kwargs)	Write this TimeSeries to a file
zip(self)	Zip the xindex and value arrays of this Series
zpk(self, zeros, poles, gain[, analog])	Filter this TimeSeries by applying a zero-pole-gain filter

Attributes Documentation

T¶

The transposed array.

Same as self.transpose().

See also

transpose

Examples

>>> x = np.array([[1.,2.],[3.,4.]])
>>> x
array([[ 1.,  2.],
       [ 3.,  4.]])
>>> x.T
array([[ 1.,  3.],
       [ 2.,  4.]])
>>> x = np.array([1.,2.,3.,4.])
>>> x
array([ 1.,  2.,  3.,  4.])
>>> x.T
array([ 1.,  2.,  3.,  4.])

base¶

Base object if memory is from some other object.

Examples

The base of an array that owns its memory is None:

>>> x = np.array([1,2,3,4])
>>> x.base is None
True

Slicing creates a view, whose memory is shared with x:

>>> y = x[2:]
>>> y.base is x
True

cgs¶

Returns a copy of the current Quantity instance with CGS units. The value of the resulting object will be scaled.

channel¶

Instrumental channel associated with these data

Type

Channel

ctypes¶

An object to simplify the interaction of the array with the ctypes module.

This attribute creates an object that makes it easier to use arrays when calling shared libraries with the ctypes module. The returned object has, among others, data, shape, and strides attributes (see Notes below) which themselves return ctypes objects that can be used as arguments to a shared library.

Parameters

None

Returns

c : Python object

Possessing attributes data, shape, strides, etc.

See also

numpy.ctypeslib

Notes

Below are the public attributes of this object which were documented in “Guide to NumPy” (we have omitted undocumented public attributes, as well as documented private attributes):

_ctypes.data

A pointer to the memory area of the array as a Python integer. This memory area may contain data that is not aligned, or not in correct byte-order. The memory area may not even be writeable. The array flags and data-type of this array should be respected when passing this attribute to arbitrary C-code to avoid trouble that can include Python crashing. User Beware! The value of this attribute is exactly the same as self._array_interface_['data'][0].

Note that unlike data_as, a reference will not be kept to the array: code like ctypes.c_void_p((a + b).ctypes.data) will result in a pointer to a deallocated array, and should be spelt (a + b).ctypes.data_as(ctypes.c_void_p)

_ctypes.shape

(c_intp*self.ndim): A ctypes array of length self.ndim where the basetype is the C-integer corresponding to dtype('p') on this platform. This base-type could be ctypes.c_int, ctypes.c_long, or ctypes.c_longlong depending on the platform. The c_intp type is defined accordingly in numpy.ctypeslib. The ctypes array contains the shape of the underlying array.

_ctypes.strides

(c_intp*self.ndim): A ctypes array of length self.ndim where the basetype is the same as for the shape attribute. This ctypes array contains the strides information from the underlying array. This strides information is important for showing how many bytes must be jumped to get to the next element in the array.

_ctypes.data_as(self, obj)

Return the data pointer cast to a particular c-types object. For example, calling self._as_parameter_ is equivalent to self.data_as(ctypes.c_void_p). Perhaps you want to use the data as a pointer to a ctypes array of floating-point data: self.data_as(ctypes.POINTER(ctypes.c_double)).

The returned pointer will keep a reference to the array.

_ctypes.shape_as(self, obj)

Return the shape tuple as an array of some other c-types type. For example: self.shape_as(ctypes.c_short).

_ctypes.strides_as(self, obj)

Return the strides tuple as an array of some other c-types type. For example: self.strides_as(ctypes.c_longlong).

If the ctypes module is not available, then the ctypes attribute of array objects still returns something useful, but ctypes objects are not returned and errors may be raised instead. In particular, the object will still have the as_parameter attribute which will return an integer equal to the data attribute.

Examples

>>> import ctypes
>>> x
array([[0, 1],
       [2, 3]])
>>> x.ctypes.data
30439712
>>> x.ctypes.data_as(ctypes.POINTER(ctypes.c_long))
<ctypes.LP_c_long object at 0x01F01300>
>>> x.ctypes.data_as(ctypes.POINTER(ctypes.c_long)).contents
c_long(0)
>>> x.ctypes.data_as(ctypes.POINTER(ctypes.c_longlong)).contents
c_longlong(4294967296L)
>>> x.ctypes.shape
<numpy.core._internal.c_long_Array_2 object at 0x01FFD580>
>>> x.ctypes.shape_as(ctypes.c_long)
<numpy.core._internal.c_long_Array_2 object at 0x01FCE620>
>>> x.ctypes.strides
<numpy.core._internal.c_long_Array_2 object at 0x01FCE620>
>>> x.ctypes.strides_as(ctypes.c_longlong)
<numpy.core._internal.c_longlong_Array_2 object at 0x01F01300>

data¶

Python buffer object pointing to the start of the array’s data.

dt¶

X-axis sample separation

Type

Quantity scalar

dtype¶

Data-type of the array’s elements.

Parameters

None

Returns

dnumpy dtype object

See also

numpy.dtype

Examples

>>> x
array([[0, 1],
       [2, 3]])
>>> x.dtype
dtype('int32')
>>> type(x.dtype)
<type 'numpy.dtype'>

duration¶

Duration of this series in seconds

Type

Quantity scalar

dx¶

X-axis sample separation

Type

Quantity scalar

epoch¶

GPS epoch for these data.

This attribute is stored internally by the t0 attribute

Type

Time

equivalencies¶

A list of equivalencies that will be applied by default during unit conversions.

flags¶

Information about the memory layout of the array.

Notes

The flags object can be accessed dictionary-like (as in a.flags['WRITEABLE']), or by using lowercased attribute names (as in a.flags.writeable). Short flag names are only supported in dictionary access.

Only the WRITEBACKIFCOPY, UPDATEIFCOPY, WRITEABLE, and ALIGNED flags can be changed by the user, via direct assignment to the attribute or dictionary entry, or by calling ndarray.setflags.

The array flags cannot be set arbitrarily:

• UPDATEIFCOPY can only be set False.

• WRITEBACKIFCOPY can only be set False.

• ALIGNED can only be set True if the data is truly aligned.

• WRITEABLE can only be set True if the array owns its own memory or the ultimate owner of the memory exposes a writeable buffer interface or is a string.

Arrays can be both C-style and Fortran-style contiguous simultaneously. This is clear for 1-dimensional arrays, but can also be true for higher dimensional arrays.

Even for contiguous arrays a stride for a given dimension arr.strides[dim] may be arbitrary if arr.shape[dim] == 1 or the array has no elements. It does not generally hold that self.strides[-1] == self.itemsize for C-style contiguous arrays or self.strides[0] == self.itemsize for Fortran-style contiguous arrays is true.

Attributes

C_CONTIGUOUS (C)

The data is in a single, C-style contiguous segment.

F_CONTIGUOUS (F)

The data is in a single, Fortran-style contiguous segment.

OWNDATA (O)

The array owns the memory it uses or borrows it from another object.

WRITEABLE (W)

The data area can be written to. Setting this to False locks the data, making it read-only. A view (slice, etc.) inherits WRITEABLE from its base array at creation time, but a view of a writeable array may be subsequently locked while the base array remains writeable. (The opposite is not true, in that a view of a locked array may not be made writeable. However, currently, locking a base object does not lock any views that already reference it, so under that circumstance it is possible to alter the contents of a locked array via a previously created writeable view onto it.) Attempting to change a non-writeable array raises a RuntimeError exception.

ALIGNED (A)

The data and all elements are aligned appropriately for the hardware.

WRITEBACKIFCOPY (X)

This array is a copy of some other array. The C-API function PyArray_ResolveWritebackIfCopy must be called before deallocating to the base array will be updated with the contents of this array.

UPDATEIFCOPY (U)

(Deprecated, use WRITEBACKIFCOPY) This array is a copy of some other array. When this array is deallocated, the base array will be updated with the contents of this array.

FNC

F_CONTIGUOUS and not C_CONTIGUOUS.

FORC

F_CONTIGUOUS or C_CONTIGUOUS (one-segment test).

BEHAVED (B)

ALIGNED and WRITEABLE.

CARRAY (CA)

BEHAVED and C_CONTIGUOUS.

FARRAY (FA)

BEHAVED and F_CONTIGUOUS and not C_CONTIGUOUS.

flat¶

A 1-D iterator over the Quantity array.

This returns a QuantityIterator instance, which behaves the same as the flatiter instance returned by flat, and is similar to, but not a subclass of, Python’s built-in iterator object.

imag¶

The imaginary part of the array.

Examples

>>> x = np.sqrt([1+0j, 0+1j])
>>> x.imag
array([ 0.        ,  0.70710678])
>>> x.imag.dtype
dtype('float64')

info(option='attributes', out='')¶

Container for meta information like name, description, format. This is required when the object is used as a mixin column within a table, but can be used as a general way to store meta information.

isscalar¶

True if the value of this quantity is a scalar, or False if it is an array-like object.

Note

This is subtly different from numpy.isscalar in that numpy.isscalar returns False for a zero-dimensional array (e.g. np.array(1)), while this is True for quantities, since quantities cannot represent true numpy scalars.

itemsize¶

Length of one array element in bytes.

Examples

>>> x = np.array([1,2,3], dtype=np.float64)
>>> x.itemsize
8
>>> x = np.array([1,2,3], dtype=np.complex128)
>>> x.itemsize
16

name¶

Name for this data set

Type

str

nbytes¶

Total bytes consumed by the elements of the array.

Notes

Does not include memory consumed by non-element attributes of the array object.

Examples

>>> x = np.zeros((3,5,2), dtype=np.complex128)
>>> x.nbytes
480
>>> np.prod(x.shape) * x.itemsize
480

ndim¶

Number of array dimensions.

Examples

>>> x = np.array([1, 2, 3])
>>> x.ndim
1
>>> y = np.zeros((2, 3, 4))
>>> y.ndim
3

real¶

The real part of the array.

See also

numpy.real

equivalent function

Examples

>>> x = np.sqrt([1+0j, 0+1j])
>>> x.real
array([ 1.        ,  0.70710678])
>>> x.real.dtype
dtype('float64')

sample_rate¶

Data rate for this TimeSeries in samples per second (Hertz).

This attribute is stored internally by the dx attribute

Type

Quantity scalar

shape¶

Tuple of array dimensions.

The shape property is usually used to get the current shape of an array, but may also be used to reshape the array in-place by assigning a tuple of array dimensions to it. As with numpy.reshape, one of the new shape dimensions can be -1, in which case its value is inferred from the size of the array and the remaining dimensions. Reshaping an array in-place will fail if a copy is required.

See also

numpy.reshape

similar function

ndarray.reshape

similar method

Examples

>>> x = np.array([1, 2, 3, 4])
>>> x.shape
(4,)
>>> y = np.zeros((2, 3, 4))
>>> y.shape
(2, 3, 4)
>>> y.shape = (3, 8)
>>> y
array([[ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.]])
>>> y.shape = (3, 6)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: total size of new array must be unchanged
>>> np.zeros((4,2))[::2].shape = (-1,)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: incompatible shape for a non-contiguous array

si¶

Returns a copy of the current Quantity instance with SI units. The value of the resulting object will be scaled.

size¶

Number of elements in the array.

Equal to np.prod(a.shape), i.e., the product of the array’s dimensions.

Notes

a.size returns a standard arbitrary precision Python integer. This may not be the case with other methods of obtaining the same value (like the suggested np.prod(a.shape), which returns an instance of np.int_), and may be relevant if the value is used further in calculations that may overflow a fixed size integer type.

Examples

>>> x = np.zeros((3, 5, 2), dtype=np.complex128)
>>> x.size
30
>>> np.prod(x.shape)
30

span¶

X-axis [low, high) segment encompassed by these data

Type

Segment

strides¶

Tuple of bytes to step in each dimension when traversing an array.

The byte offset of element (i[0], i[1], ..., i[n]) in an array a is:

offset = sum(np.array(i) * a.strides)

A more detailed explanation of strides can be found in the “ndarray.rst” file in the NumPy reference guide.

See also

numpy.lib.stride_tricks.as_strided

Notes

Imagine an array of 32-bit integers (each 4 bytes):

x = np.array([[0, 1, 2, 3, 4],
              [5, 6, 7, 8, 9]], dtype=np.int32)

This array is stored in memory as 40 bytes, one after the other (known as a contiguous block of memory). The strides of an array tell us how many bytes we have to skip in memory to move to the next position along a certain axis. For example, we have to skip 4 bytes (1 value) to move to the next column, but 20 bytes (5 values) to get to the same position in the next row. As such, the strides for the array x will be (20, 4).

Examples

>>> y = np.reshape(np.arange(2*3*4), (2,3,4))
>>> y
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],
       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
>>> y.strides
(48, 16, 4)
>>> y[1,1,1]
17
>>> offset=sum(y.strides * np.array((1,1,1)))
>>> offset/y.itemsize
17

>>> x = np.reshape(np.arange(5*6*7*8), (5,6,7,8)).transpose(2,3,1,0)
>>> x.strides
(32, 4, 224, 1344)
>>> i = np.array([3,5,2,2])
>>> offset = sum(i * x.strides)
>>> x[3,5,2,2]
813
>>> offset / x.itemsize
813

t0¶

X-axis coordinate of the first data point

Type

Quantity scalar

times¶

Positions of the data on the x-axis

Type

Quantity array

unit¶

The physical unit of these data

Type

UnitBase

value¶

The numerical value of this instance.

See also

to_value

Get the numerical value in a given unit.

x0¶

X-axis coordinate of the first data point

Type

Quantity scalar

xindex¶

Positions of the data on the x-axis

Type

Quantity array

xspan¶

X-axis [low, high) segment encompassed by these data

Type

Segment

xunit¶

Unit of x-axis index

Type

Unit

Methods Documentation

abs(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj])[source]¶

Calculate the absolute value element-wise.

np.abs is a shorthand for this function.

Parameters

x : array_like

Input array.

out : ndarray, None, or tuple of ndarray and None, optional

A location into which the result is stored. If provided, it must have a shape that the inputs broadcast to. If not provided or None, a freshly-allocated array is returned. A tuple (possible only as a keyword argument) must have length equal to the number of outputs.

where : array_like, optional

This condition is broadcast over the input. At locations where the condition is True, the out array will be set to the ufunc result. Elsewhere, the out array will retain its original value. Note that if an uninitialized out array is created via the default out=None, locations within it where the condition is False will remain uninitialized.

**kwargs

For other keyword-only arguments, see the ufunc docs.

Returns

absolute : ndarray

An ndarray containing the absolute value of each element in x. For complex input, a + ib, the absolute value is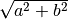 . This is a scalar if x is a scalar.

Examples

>>> x = np.array([-1.2, 1.2])
>>> np.absolute(x)
array([ 1.2,  1.2])
>>> np.absolute(1.2 + 1j)
1.5620499351813308

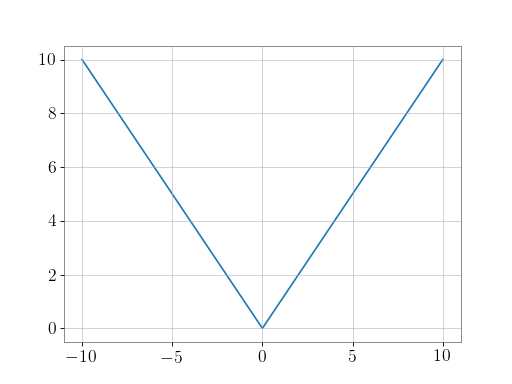
Plot the function over [-10, 10]:

>>> import matplotlib.pyplot as plt

>>> x = np.linspace(start=-10, stop=10, num=101)
>>> plt.plot(x, np.absolute(x))
>>> plt.show()

(png)

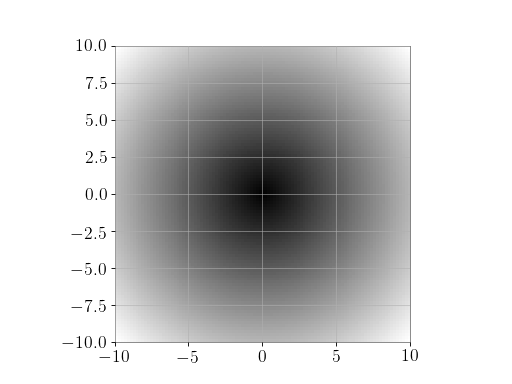
Plot the function over the complex plane:

>>> xx = x + 1j * x[:, np.newaxis]
>>> plt.imshow(np.abs(xx), extent=[-10, 10, -10, 10], cmap='gray')
>>> plt.show()

(png)

all(axis=None, out=None, keepdims=False)¶

Returns True if all elements evaluate to True.

Refer to numpy.all for full documentation.

See also

numpy.all

equivalent function

any(axis=None, out=None, keepdims=False)¶

Returns True if any of the elements of a evaluate to True.

Refer to numpy.any for full documentation.

See also

numpy.any

equivalent function

append(self, other, inplace=True, pad=None, gap=None, resize=True)[source]¶

Connect another series onto the end of the current one.

Parameters

other : Series

another series of the same type to connect to this one

inplace : bool, optional

perform operation in-place, modifying current series, otherwise copy data and return new series, default: True

Warning

inplace append bypasses the reference check in numpy.ndarray.resize, so be carefully to only use this for arrays that haven’t been sharing their memory!

pad : float, optional

value with which to pad discontiguous series, by default gaps will result in a ValueError.

gap : str, optional

action to perform if there’s a gap between the other series and this one. One of

• 'raise' - raise a ValueError

• 'ignore' - remove gap and join data

• 'pad' - pad gap with zeros

If pad is given and is not None, the default is 'pad', otherwise 'raise'. If gap='pad' is given, the default for pad is 0.

resize : bool, optional

resize this array to accommodate new data, otherwise shift the old data to the left (potentially falling off the start) and put the new data in at the end, default: True.

Returns

series : Series

a new series containing joined data sets

argmax(axis=None, out=None)¶

Return indices of the maximum values along the given axis.

Refer to numpy.argmax for full documentation.

See also

numpy.argmax

equivalent function

argmin(axis=None, out=None)¶

Return indices of the minimum values along the given axis of a.

Refer to numpy.argmin for detailed documentation.

See also

numpy.argmin

equivalent function

argpartition(kth, axis=-1, kind='introselect', order=None)¶

Returns the indices that would partition this array.

Refer to numpy.argpartition for full documentation.

New in version 1.8.0.

See also

numpy.argpartition

equivalent function

argsort(axis=-1, kind=None, order=None)¶

Returns the indices that would sort this array.

Refer to numpy.argsort for full documentation.

See also

numpy.argsort

equivalent function

asd(self, fftlength=None, overlap=None, window='hann', method='welch', **kwargs)[source]¶

Calculate the ASD FrequencySeries of this TimeSeries

Parameters

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

method : str, optional

FFT-averaging method, see Notes for more details

Returns

psd : FrequencySeries

a data series containing the PSD.

See also

TimeSeries.psd

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

astype(dtype, order='K', casting='unsafe', subok=True, copy=True)¶

Copy of the array, cast to a specified type.

Parameters

dtype : str or dtype

Typecode or data-type to which the array is cast.

order : {‘C’, ‘F’, ‘A’, ‘K’}, optional

Controls the memory layout order of the result. ‘C’ means C order, ‘F’ means Fortran order, ‘A’ means ‘F’ order if all the arrays are Fortran contiguous, ‘C’ order otherwise, and ‘K’ means as close to the order the array elements appear in memory as possible. Default is ‘K’.

casting : {‘no’, ‘equiv’, ‘safe’, ‘same_kind’, ‘unsafe’}, optional

Controls what kind of data casting may occur. Defaults to ‘unsafe’ for backwards compatibility.

• ‘no’ means the data types should not be cast at all.

• ‘equiv’ means only byte-order changes are allowed.

• ‘safe’ means only casts which can preserve values are allowed.

• ‘same_kind’ means only safe casts or casts within a kind, like float64 to float32, are allowed.

• ‘unsafe’ means any data conversions may be done.

subok : bool, optional

If True, then sub-classes will be passed-through (default), otherwise the returned array will be forced to be a base-class array.

copy : bool, optional

By default, astype always returns a newly allocated array. If this is set to false, and the dtype, order, and subok requirements are satisfied, the input array is returned instead of a copy.

Returns

arr_t : ndarray

Unless copy is False and the other conditions for returning the input array are satisfied (see description for copy input parameter), arr_t is a new array of the same shape as the input array, with dtype, order given by dtype, order.

Raises

ComplexWarning

When casting from complex to float or int. To avoid this, one should use a.real.astype(t).

Notes

Changed in version 1.17.0: Casting between a simple data type and a structured one is possible only for “unsafe” casting. Casting to multiple fields is allowed, but casting from multiple fields is not.

Changed in version 1.9.0: Casting from numeric to string types in ‘safe’ casting mode requires that the string dtype length is long enough to store the max integer/float value converted.

Examples

>>> x = np.array([1, 2, 2.5])
>>> x
array([1. ,  2. ,  2.5])

>>> x.astype(int)
array([1, 2, 2])

auto_coherence(self, dt, fftlength=None, overlap=None, window='hann', **kwargs)[source]¶

Calculate the frequency-coherence between this TimeSeries and a time-shifted copy of itself.

The standard TimeSeries.coherence() is calculated between the input TimeSeries and a cropped copy of itself. Since the cropped version will be shorter, the input series will be shortened to match.

Parameters

dt : float

duration (in seconds) of time-shift

fftlength : float, optional

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

**kwargs

any other keyword arguments accepted by matplotlib.mlab.cohere() except NFFT, window, and noverlap which are superceded by the above keyword arguments

Returns

coherence : FrequencySeries

the coherence FrequencySeries of this TimeSeries with the other

See also

matplotlib.mlab.cohere

for details of the coherence calculator

Notes

The TimeSeries.auto_coherence() will perform best when dt is approximately fftlength / 2.

average_fft(self, fftlength=None, overlap=0, window=None)[source]¶

Compute the averaged one-dimensional DFT of this TimeSeries.

This method computes a number of FFTs of duration fftlength and overlap (both given in seconds), and returns the mean average. This method is analogous to the Welch average method for power spectra.

Parameters

fftlength : float

number of seconds in single FFT, default, use whole TimeSeries

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

Returns

out : complex-valued FrequencySeries

the transformed output, with populated frequencies array metadata

See also

TimeSeries.fft

The FFT method used.

bandpass(self, flow, fhigh, gpass=2, gstop=30, fstop=None, type='iir', filtfilt=True, **kwargs)[source]¶

Filter this TimeSeries with a band-pass filter.

Parameters

flow : float

lower corner frequency of pass band

fhigh : float

upper corner frequency of pass band

gpass : float

the maximum loss in the passband (dB).

gstop : float

the minimum attenuation in the stopband (dB).

fstop : tuple of float, optional

(low, high) edge-frequencies of stop band

type : str

the filter type, either 'iir' or 'fir'

**kwargs

other keyword arguments are passed to gwpy.signal.filter_design.bandpass()

Returns

bpseries : TimeSeries

a band-passed version of the input TimeSeries

See also

gwpy.signal.filter_design.bandpass

for details on the filter design

TimeSeries.filter

for details on how the filter is applied

Notes

When using scipy < 0.16.0 some higher-order filters may be unstable. With scipy >= 0.16.0 higher-order filters are decomposed into second-order-sections, and so are much more stable.

byteswap(inplace=False)¶

Swap the bytes of the array elements

Toggle between low-endian and big-endian data representation by returning a byteswapped array, optionally swapped in-place.

Parameters

inplace : bool, optional

If True, swap bytes in-place, default is False.

Returns

out : ndarray

The byteswapped array. If inplace is True, this is a view to self.

Examples

>>> A = np.array([1, 256, 8755], dtype=np.int16)
>>> list(map(hex, A))
['0x1', '0x100', '0x2233']
>>> A.byteswap(inplace=True)
array([  256,     1, 13090], dtype=int16)
>>> list(map(hex, A))
['0x100', '0x1', '0x3322']

Arrays of strings are not swapped

>>> A = np.array(['ceg', 'fac'])
>>> A.byteswap()
Traceback (most recent call last):
    ...
UnicodeDecodeError: ...

choose(choices, out=None, mode='raise')¶

Use an index array to construct a new array from a set of choices.

Refer to numpy.choose for full documentation.

See also

numpy.choose

equivalent function

clip(min=None, max=None, out=None, **kwargs)¶

Return an array whose values are limited to [min, max]. One of max or min must be given.

Refer to numpy.clip for full documentation.

See also

numpy.clip

equivalent function

coherence(self, other, fftlength=None, overlap=None, window='hann', **kwargs)[source]¶

Calculate the frequency-coherence between this TimeSeries and another.

Parameters

other : TimeSeries

TimeSeries signal to calculate coherence with

fftlength : float, optional

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

**kwargs

any other keyword arguments accepted by matplotlib.mlab.cohere() except NFFT, window, and noverlap which are superceded by the above keyword arguments

Returns

coherence : FrequencySeries

the coherence FrequencySeries of this TimeSeries with the other

See also

matplotlib.mlab.cohere

for details of the coherence calculator

Notes

If self and other have difference TimeSeries.sample_rate values, the higher sampled TimeSeries will be down-sampled to match the lower.

coherence_spectrogram(self, other, stride, fftlength=None, overlap=None, window='hann', nproc=1)[source]¶

Calculate the coherence spectrogram between this TimeSeries and other.

Parameters

other : TimeSeries

the second TimeSeries in this CSD calculation

stride : float

number of seconds in single PSD (column of spectrogram)

fftlength : float

number of seconds in single FFT

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

nproc : int

number of parallel processes to use when calculating individual coherence spectra.

Returns

spectrogram : Spectrogram

time-frequency coherence spectrogram as generated from the input time-series.

compress(condition, axis=None, out=None)¶

Return selected slices of this array along given axis.

Refer to numpy.compress for full documentation.

See also

numpy.compress

equivalent function

conj()¶

Complex-conjugate all elements.

Refer to numpy.conjugate for full documentation.

See also

numpy.conjugate

equivalent function

conjugate()¶

Return the complex conjugate, element-wise.

Refer to numpy.conjugate for full documentation.

See also

numpy.conjugate

equivalent function

convolve(self, fir, window='hanning')[source]¶

Convolve this TimeSeries with an FIR filter using the

overlap-save method

Parameters

fir : numpy.ndarray

the time domain filter to convolve with

window : str, optional

window function to apply to boundaries, default: 'hanning' see scipy.signal.get_window() for details on acceptable formats

Returns

out : TimeSeries

the result of the convolution

See also

scipy.signal.fftconvolve

for details on the convolution scheme used here

TimeSeries.filter

for an alternative method designed for short filters

Notes

The output TimeSeries is the same length and has the same timestamps as the input.

Due to filter settle-in, a segment half the length of fir will be corrupted at the left and right boundaries. To prevent spectral leakage these segments will be windowed before convolving.

copy(order='C')[source]¶

Return a copy of the array.

Parameters

order : {‘C’, ‘F’, ‘A’, ‘K’}, optional

Controls the memory layout of the copy. ‘C’ means C-order, ‘F’ means F-order, ‘A’ means ‘F’ if a is Fortran contiguous, ‘C’ otherwise. ‘K’ means match the layout of a as closely as possible. (Note that this function and numpy.copy() are very similar, but have different default values for their order= arguments.)

See also

numpy.copy

numpy.copyto

Examples

>>> x = np.array([[1,2,3],[4,5,6]], order='F')

>>> y = x.copy()

>>> x.fill(0)

>>> x
array([[0, 0, 0],
       [0, 0, 0]])

>>> y
array([[1, 2, 3],
       [4, 5, 6]])

>>> y.flags['C_CONTIGUOUS']
True

correlate(self, mfilter, window='hanning', detrend='linear', whiten=False, wduration=2, highpass=None, **asd_kw)[source]¶

Cross-correlate this TimeSeries with another signal

Parameters

mfilter : TimeSeries

the time domain signal to correlate with

window : str, optional

window function to apply to timeseries prior to FFT, default: 'hanning' see scipy.signal.get_window() for details on acceptable formats

detrend : str, optional

type of detrending to do before FFT (see detrend for more details), default: 'linear'

whiten : bool, optional

boolean switch to enable (True) or disable (False) data whitening, default: False

wduration : float, optional

duration (in seconds) of the time-domain FIR whitening filter, only used if whiten=True, defaults to 2 seconds

highpass : float, optional

highpass corner frequency (in Hz) of the FIR whitening filter, only used if whiten=True, default: None

**asd_kw

keyword arguments to pass to TimeSeries.asd to generate an ASD, only used if whiten=True

Returns

snr : TimeSeries

the correlated signal-to-noise ratio (SNR) timeseries

See also

TimeSeries.asd

for details on the ASD calculation

TimeSeries.convolve

for details on convolution with the overlap-save method

Notes

The window argument is used in ASD estimation, whitening, and preventing spectral leakage in the output. It is not used to condition the matched-filter, which should be windowed before passing to this method.

Due to filter settle-in, a segment half the length of mfilter will be corrupted at the beginning and end of the output. See convolve for more details.

The input and matched-filter will be detrended, and the output will be normalised so that the SNR measures number of standard deviations from the expected mean.

crop(self, start=None, end=None, copy=False)[source]¶

Crop this series to the given x-axis extent.

Parameters

start : float, optional

lower limit of x-axis to crop to, defaults to current x0

end : float, optional

upper limit of x-axis to crop to, defaults to current series end

copy : bool, optional, default: False

copy the input data to fresh memory, otherwise return a view

Returns

series : Series

A new series with a sub-set of the input data

Notes

If either start or end are outside of the original Series span, warnings will be printed and the limits will be restricted to the xspan

csd(self, other, fftlength=None, overlap=None, window='hann', **kwargs)[source]¶

Calculate the CSD FrequencySeries for two TimeSeries

Parameters

other : TimeSeries

the second TimeSeries in this CSD calculation

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

Returns

csd : FrequencySeries

a data series containing the CSD.

csd_spectrogram(self, other, stride, fftlength=None, overlap=0, window='hann', nproc=1, **kwargs)[source]¶

Calculate the cross spectral density spectrogram of this

TimeSeries with ‘other’.

Parameters

other : TimeSeries

second time-series for cross spectral density calculation

stride : float

number of seconds in single PSD (column of spectrogram).

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

nproc : int

maximum number of independent frame reading processes, default is set to single-process file reading.

Returns

spectrogram : Spectrogram

time-frequency cross spectrogram as generated from the two input time-series.

cumprod(axis=None, dtype=None, out=None)¶

Return the cumulative product of the elements along the given axis.

Refer to numpy.cumprod for full documentation.

See also

numpy.cumprod

equivalent function

cumsum(axis=None, dtype=None, out=None)¶

Return the cumulative sum of the elements along the given axis.

Refer to numpy.cumsum for full documentation.

See also

numpy.cumsum

equivalent function

decompose(self, bases=[])¶

Generates a new Quantity with the units decomposed. Decomposed units have only irreducible units in them (see astropy.units.UnitBase.decompose).

Parameters

bases : sequence of UnitBase, optional

The bases to decompose into. When not provided, decomposes down to any irreducible units. When provided, the decomposed result will only contain the given units. This will raises a UnitsError if it’s not possible to do so.

Returns

newq : Quantity

A new object equal to this quantity with units decomposed.

demodulate(self, f, stride=1, exp=False, deg=True)[source]¶

Compute the average magnitude and phase of this TimeSeries once per stride at a given frequency

Parameters

f : float

frequency (Hz) at which to demodulate the signal

stride : float, optional

stride (seconds) between calculations, defaults to 1 second

exp : bool, optional

return the magnitude and phase trends as one TimeSeries object representing a complex exponential, default: False

deg : bool, optional

if exp=False, calculates the phase in degrees

Returns

mag, phase : TimeSeries

if exp=False, returns a pair of TimeSeries objects representing magnitude and phase trends with dt=stride

out : TimeSeries

if exp=True, returns a single TimeSeries with magnitude and phase trends represented as mag * exp(1j*phase) with dt=stride

See also

TimeSeries.heterodyne

for the underlying heterodyne detection method

Examples

Demodulation is useful when trying to examine steady sinusoidal signals we know to be contained within data. For instance, we can download some data from LOSC to look at trends of the amplitude and phase of LIGO Livingston’s calibration line at 331.3 Hz:

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('L1', 1131350417, 1131357617)

We can demodulate the TimeSeries at 331.3 Hz with a stride of one minute:

>>> amp, phase = data.demodulate(331.3, stride=60)

We can then plot these trends to visualize fluctuations in the amplitude of the calibration line:

>>> from gwpy.plot import Plot
>>> plot = Plot(amp)
>>> ax = plot.gca()
>>> ax.set_ylabel('Strain Amplitude at 331.3 Hz')
>>> plot.show()

(png)

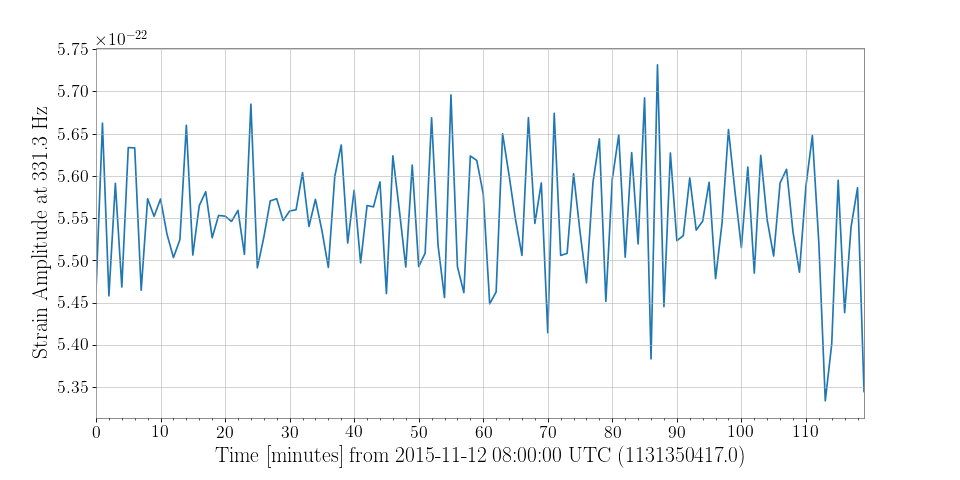
detrend(self, detrend='constant')[source]¶

Remove the trend from this TimeSeries

This method just wraps scipy.signal.detrend() to return an object of the same type as the input.

Parameters

detrend : str, optional

the type of detrending.

Returns

detrended : TimeSeries

the detrended input series

See also

scipy.signal.detrend

for details on the options for the detrend argument, and how the operation is done

diagonal(offset=0, axis1=0, axis2=1)¶

Return specified diagonals. In NumPy 1.9 the returned array is a read-only view instead of a copy as in previous NumPy versions. In a future version the read-only restriction will be removed.

Refer to numpy.diagonal() for full documentation.

See also

numpy.diagonal

equivalent function

diff(self, n=1, axis=-1)[source]¶

Calculate the n-th order discrete difference along given axis.

The first order difference is given by out[n] = a[n+1] - a[n] along the given axis, higher order differences are calculated by using diff recursively.

Parameters

n : int, optional

The number of times values are differenced.

axis : int, optional

The axis along which the difference is taken, default is the last axis.

Returns

diff : Series

The n order differences. The shape of the output is the same as the input, except along axis where the dimension is smaller by n.

See also

numpy.diff

for documentation on the underlying method

dot(b, out=None)¶

Dot product of two arrays.

Refer to numpy.dot for full documentation.

See also

numpy.dot

equivalent function

Examples

>>> a = np.eye(2)
>>> b = np.ones((2, 2)) * 2
>>> a.dot(b)
array([[2.,  2.],
       [2.,  2.]])

This array method can be conveniently chained:

>>> a.dot(b).dot(b)
array([[8.,  8.],
       [8.,  8.]])

dump(file)¶

Dump a pickle of the array to the specified file. The array can be read back with pickle.load or numpy.load.

Parameters

file : str or Path

A string naming the dump file.

Changed in version 1.17.0: pathlib.Path objects are now accepted.

dumps()[source]¶

Returns the pickle of the array as a string. pickle.loads or numpy.loads will convert the string back to an array.

Parameters

None

ediff1d(self, to_end=None, to_begin=None)¶

classmethod fetch(channel, start, end, host=None, port=None, verbose=False, connection=None, verify=False, pad=None, allow_tape=None, scaled=None, type=None, dtype=None)[source]¶

Fetch data from NDS

Parameters

channel : str, Channel

the data channel for which to query

start : LIGOTimeGPS, float, str

GPS start time of required data, any input parseable by to_gps is fine

end : LIGOTimeGPS, float, str

GPS end time of required data, any input parseable by to_gps is fine

host : str, optional

URL of NDS server to use, if blank will try any server (in a relatively sensible order) to get the data

port : int, optional

port number for NDS server query, must be given with host

verify : bool, optional, default: False

check channels exist in database before asking for data

scaled : bool, optional

apply slope and bias calibration to ADC data, for non-ADC data this option has no effect

connection : nds2.connection, optional

open NDS connection to use

verbose : bool, optional

print verbose output about NDS progress, useful for debugging; if verbose is specified as a string, this defines the prefix for the progress meter

type : int, optional

NDS2 channel type integer

dtype : type, numpy.dtype, str, optional

identifier for desired output data type

classmethod fetch_open_data(ifo, start, end, sample_rate=4096, tag=None, version=None, format='hdf5', host='https://www.gw-openscience.org', verbose=False, cache=None, **kwargs)[source]¶

Fetch open-access data from the LIGO Open Science Center

Parameters

ifo : str

the two-character prefix of the IFO in which you are interested, e.g. 'L1'

start : LIGOTimeGPS, float, str, optional

GPS start time of required data, defaults to start of data found; any input parseable by to_gps is fine

end : LIGOTimeGPS, float, str, optional

GPS end time of required data, defaults to end of data found; any input parseable by to_gps is fine

sample_rate : float, optional,

the sample rate of desired data; most data are stored by LOSC at 4096 Hz, however there may be event-related data releases with a 16384 Hz rate, default: 4096

tag : str, optional

file tag, e.g. 'CLN' to select cleaned data, or 'C00' for ‘raw’ calibrated data.

version : int, optional

version of files to download, defaults to highest discovered version

format : str, optional

the data format to download and parse, default: 'h5py'

• 'hdf5'

• 'gwf' - requires LDAStools.frameCPP

host : str, optional

HTTP host name of LOSC server to access

verbose : bool, optional, default: False

print verbose output while fetching data

cache : bool, optional

save/read a local copy of the remote URL, default: False; useful if the same remote data are to be accessed multiple times. Set GWPY_CACHE=1 in the environment to auto-cache.

**kwargs

any other keyword arguments are passed to the TimeSeries.read method that parses the file that was downloaded

Notes

StateVector data are not available in txt.gz format.

Examples

>>> from gwpy.timeseries import (TimeSeries, StateVector)
>>> print(TimeSeries.fetch_open_data('H1', 1126259446, 1126259478))
TimeSeries([  2.17704028e-19,  2.08763900e-19,  2.39681183e-19,
            ...,   3.55365541e-20,  6.33533516e-20,
              7.58121195e-20]
           unit: Unit(dimensionless),
           t0: 1126259446.0 s,
           dt: 0.000244140625 s,
           name: Strain,
           channel: None)
>>> print(StateVector.fetch_open_data('H1', 1126259446, 1126259478))
StateVector([127,127,127,127,127,127,127,127,127,127,127,127,
             127,127,127,127,127,127,127,127,127,127,127,127,
             127,127,127,127,127,127,127,127]
            unit: Unit(dimensionless),
            t0: 1126259446.0 s,
            dt: 1.0 s,
            name: Data quality,
            channel: None,
            bits: Bits(0: data present
                       1: passes cbc CAT1 test
                       2: passes cbc CAT2 test
                       3: passes cbc CAT3 test
                       4: passes burst CAT1 test
                       5: passes burst CAT2 test
                       6: passes burst CAT3 test,
                       channel=None,
                       epoch=1126259446.0))

For the StateVector, the naming of the bits will be format-dependent, because they are recorded differently by LOSC in different formats.

For events published in O2 and later, LOSC typically provides multiple data sets containing the original ('C00') and cleaned ('CLN') data. To select both data sets and plot a comparison, for example:

>>> orig = TimeSeries.fetch_open_data('H1', 1187008870, 1187008896,
...                                   tag='C00')
>>> cln = TimeSeries.fetch_open_data('H1', 1187008870, 1187008896,
...                                  tag='CLN')
>>> origasd = orig.asd(fftlength=4, overlap=2)
>>> clnasd = cln.asd(fftlength=4, overlap=2)
>>> plot = origasd.plot(label='Un-cleaned')
>>> ax = plot.gca()
>>> ax.plot(clnasd, label='Cleaned')
>>> ax.set_xlim(10, 1400)
>>> ax.set_ylim(1e-24, 1e-20)
>>> ax.legend()
>>> plot.show()

(png)

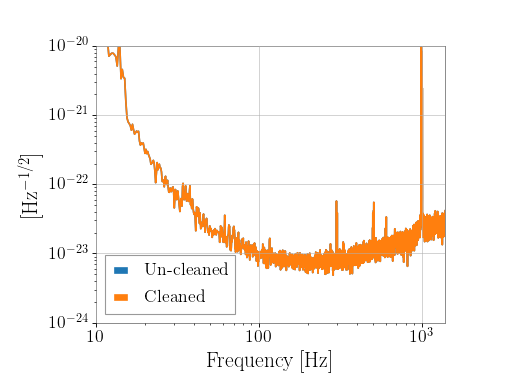
fft(self, nfft=None)[source]¶

Compute the one-dimensional discrete Fourier transform of this TimeSeries.

Parameters

nfft : int, optional

length of the desired Fourier transform, input will be cropped or padded to match the desired length. If nfft is not given, the length of the TimeSeries will be used

Returns

out : FrequencySeries

the normalised, complex-valued FFT FrequencySeries.

See also

numpy.fft.rfft

The FFT implementation used in this method.

Notes

This method, in constrast to the numpy.fft.rfft() method it calls, applies the necessary normalisation such that the amplitude of the output FrequencySeries is correct.

fftgram(self, fftlength, overlap=None, window='hann', **kwargs)[source]¶

Calculate the Fourier-gram of this TimeSeries.

At every stride, a single, complex FFT is calculated.

Parameters

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable

Returns

a Fourier-gram

fill(value)¶

Fill the array with a scalar value.

Parameters

value : scalar

All elements of a will be assigned this value.

Examples

>>> a = np.array([1, 2])
>>> a.fill(0)
>>> a
array([0, 0])
>>> a = np.empty(2)
>>> a.fill(1)
>>> a
array([1.,  1.])

filter(self, *filt, **kwargs)[source]¶

Filter this TimeSeries with an IIR or FIR filter

Parameters

*filt : filter arguments

1, 2, 3, or 4 arguments defining the filter to be applied,

• an Nx1 ndarray of FIR coefficients

• an Nx6 ndarray of SOS coefficients

• (numerator, denominator) polynomials

• (zeros, poles, gain)

• (A, B, C, D) ‘state-space’ representation

filtfilt : bool, optional

filter forward and backwards to preserve phase, default: False

analog : bool, optional

if True, filter coefficients will be converted from Hz to Z-domain digital representation, default: False

inplace : bool, optional

if True, this array will be overwritten with the filtered version, default: False

**kwargs

other keyword arguments are passed to the filter method

Returns

result : TimeSeries

the filtered version of the input TimeSeries

Raises

ValueError

if filt arguments cannot be interpreted properly

See also

scipy.signal.sosfilt

for details on filtering with second-order sections (scipy >= 0.16 only)

scipy.signal.sosfiltfilt

for details on forward-backward filtering with second-order sections (scipy >= 0.18 only)

scipy.signal.lfilter

for details on filtering (without SOS)

scipy.signal.filtfilt

for details on forward-backward filtering (without SOS)

Notes

IIR filters are converted either into cascading second-order sections (if scipy >= 0.16 is installed), or into the (numerator, denominator) representation before being applied to this TimeSeries.

When using scipy < 0.16 some higher-order filters may be unstable. With scipy >= 0.16 higher-order filters are decomposed into second-order-sections, and so are much more stable.

FIR filters are passed directly to scipy.signal.lfilter() or scipy.signal.filtfilt() without any conversions.

Examples

We can design an arbitrarily complicated filter using gwpy.signal.filter_design

>>> from gwpy.signal import filter_design
>>> bp = filter_design.bandpass(50, 250, 4096.)
>>> notches = [filter_design.notch(f, 4096.) for f in (60, 120, 180)]
>>> zpk = filter_design.concatenate_zpks(bp, *notches)

And then can download some data from LOSC to apply it using TimeSeries.filter:

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('H1', 1126259446, 1126259478)
>>> filtered = data.filter(zpk, filtfilt=True)

We can plot the original signal, and the filtered version, cutting off either end of the filtered data to remove filter-edge artefacts

>>> from gwpy.plot import Plot
>>> plot = Plot(data, filtered[128:-128], separate=True)
>>> plot.show()

(png)

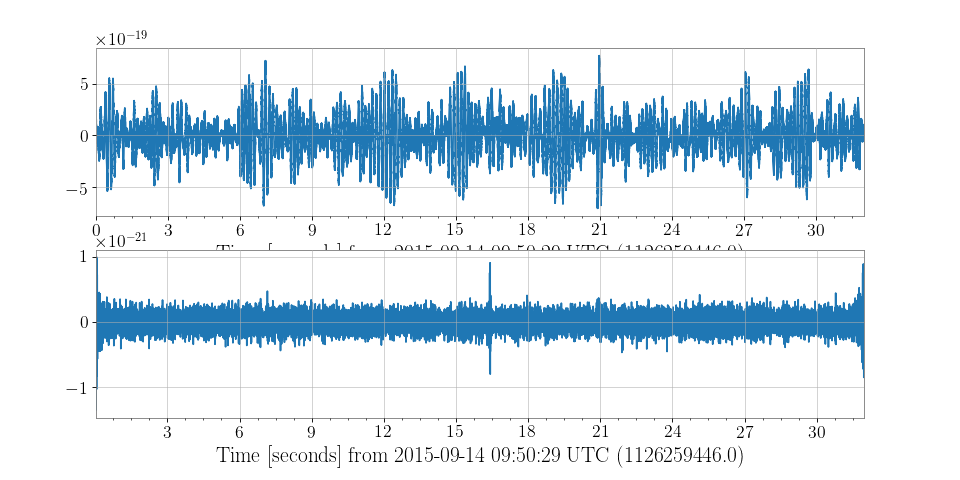
classmethod find(channel, start, end, frametype=None, pad=None, scaled=None, dtype=None, nproc=1, verbose=False, **readargs)[source]¶

Find and read data from frames for a channel

Parameters

channel : str, Channel

the name of the channel to read, or a Channel object.

start : LIGOTimeGPS, float, str

GPS start time of required data, any input parseable by to_gps is fine

end : LIGOTimeGPS, float, str

GPS end time of required data, any input parseable by to_gps is fine

frametype : str, optional

name of frametype in which this channel is stored, will search for containing frame types if necessary

nproc : int, optional, default: 1

number of parallel processes to use, serial process by default.

pad : float, optional

value with which to fill gaps in the source data, by default gaps will result in a ValueError.

dtype : numpy.dtype, str, type, or dict

numeric data type for returned data, e.g. numpy.float, or dict of (channel, dtype) pairs

allow_tape : bool, optional, default: True

allow reading from frame files on (slow) magnetic tape

verbose : bool, optional

print verbose output about read progress, if verbose is specified as a string, this defines the prefix for the progress meter

**readargs

any other keyword arguments to be passed to read()

flatten(self, order='C')[source]¶

Return a copy of the array collapsed into one dimension.

Any index information is removed as part of the flattening, and the result is returned as a Quantity array.

Parameters

order : {‘C’, ‘F’, ‘A’, ‘K’}, optional

‘C’ means to flatten in row-major (C-style) order. ‘F’ means to flatten in column-major (Fortran- style) order. ‘A’ means to flatten in column-major order if a is Fortran contiguous in memory, row-major order otherwise. ‘K’ means to flatten a in the order the elements occur in memory. The default is ‘C’.

Returns

y : Quantity

A copy of the input array, flattened to one dimension.

See also

ravel

Return a flattened array.

flat

A 1-D flat iterator over the array.

Examples

>>> a = Array([[1,2], [3,4]], unit='m', name='Test')
>>> a.flatten()
<Quantity [1., 2., 3., 4.] m>

classmethod from_lal(lalts, copy=True)[source]¶

Generate a new TimeSeries from a LAL TimeSeries of any type.

classmethod from_nds2_buffer(buffer_, scaled=None, copy=True, **metadata)[source]¶

Construct a new series from an nds2.buffer object

Requires: nds2

Parameters

buffer_ : nds2.buffer

the input NDS2-client buffer to read

scaled : bool, optional

apply slope and bias calibration to ADC data, for non-ADC data this option has no effect

copy : bool, optional

if True, copy the contained data array to new to a new array

**metadata

any other metadata keyword arguments to pass to the TimeSeries constructor

Returns

timeseries : TimeSeries

a new TimeSeries containing the data from the nds2.buffer, and the appropriate metadata

classmethod from_pycbc(pycbcseries, copy=True)[source]¶

Convert a pycbc.types.timeseries.TimeSeries into a TimeSeries

Parameters

pycbcseries : pycbc.types.timeseries.TimeSeries

the input PyCBC TimeSeries array

copy : bool, optional, default: True

if True, copy these data to a new array

Returns

timeseries : TimeSeries

a GWpy version of the input timeseries

gate(self, tzero=1.0, tpad=0.5, whiten=True, threshold=50.0, cluster_window=0.5, **whiten_kwargs)[source]¶

Removes high amplitude peaks from data using inverse Planck window.

Points will be discovered automatically using a provided threshold and clustered within a provided time window.

Parameters

tzero : int, optional

half-width time duration in which the time series is set to zero

tpad : int, optional

half-width time duration in which the Planck window is tapered

whiten : bool, optional

if True, data will be whitened before gating points are discovered, use of this option is highly recommended

threshold : float, optional

amplitude threshold, if the data exceeds this value a gating window will be placed

cluster_window : float, optional

time duration over which gating points will be clustered

**whiten_kwargs

other keyword arguments that will be passed to the TimeSeries.whiten method if it is being used when discovering gating points

Returns

out : TimeSeries

a copy of the original TimeSeries that has had gating windows applied

Examples

Read data into a TimeSeries

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('H1', 1135148571, 1135148771)

Apply gating using custom arguments

>>> gated = data.gate(tzero=1.0, tpad=1.0, threshold=10.0,
                      fftlength=4, overlap=2, method='median')

Plot the original data and the gated data, whiten both for visualization purposes

>>> overlay = data.whiten(4,2,method='median').plot(dpi=150,
                          label='Ungated', color='dodgerblue',
                          zorder=2)
>>> ax = overlay.gca()
>>> ax.plot(gated.whiten(4,2,method='median'), label='Gated',
            color='orange', zorder=3)
>>> ax.set_xlim(1135148661, 1135148681)
>>> ax.legend()
>>> overlay.show()

classmethod get(channel, start, end, pad=None, scaled=None, dtype=None, verbose=False, allow_tape=None, **kwargs)[source]¶

Get data for this channel from frames or NDS

This method dynamically accesses either frames on disk, or a remote NDS2 server to find and return data for the given interval

Parameters

channel : str, Channel

the name of the channel to read, or a Channel object.

start : LIGOTimeGPS, float, str

GPS start time of required data, any input parseable by to_gps is fine

end : LIGOTimeGPS, float, str

GPS end time of required data, any input parseable by to_gps is fine

pad : float, optional

value with which to fill gaps in the source data, by default gaps will result in a ValueError.

scaled : bool, optional

apply slope and bias calibration to ADC data, for non-ADC data this option has no effect

dtype : numpy.dtype, str, type, or dict

numeric data type for returned data, e.g. numpy.float, or dict of (channel, dtype) pairs

nproc : int, optional, default: 1

number of parallel processes to use, serial process by default.

allow_tape : bool, optional, default: None

allow the use of frames that are held on tape, default is None to attempt to allow the TimeSeries.fetch method to intelligently select a server that doesn’t use tapes for data storage (doesn’t always work), but to eventually allow retrieving data from tape if required

verbose : bool, optional

print verbose output about data access progress, if verbose is specified as a string, this defines the prefix for the progress meter

**kwargs

other keyword arguments to pass to either find() (for direct GWF file access) or fetch() for remote NDS2 access

See also

TimeSeries.fetch

for grabbing data from a remote NDS2 server

TimeSeries.find

for discovering and reading data from local GWF files

getfield(dtype, offset=0)¶

Returns a field of the given array as a certain type.

A field is a view of the array data with a given data-type. The values in the view are determined by the given type and the offset into the current array in bytes. The offset needs to be such that the view dtype fits in the array dtype; for example an array of dtype complex128 has 16-byte elements. If taking a view with a 32-bit integer (4 bytes), the offset needs to be between 0 and 12 bytes.

Parameters

dtype : str or dtype

The data type of the view. The dtype size of the view can not be larger than that of the array itself.

offset : int

Number of bytes to skip before beginning the element view.

Examples

>>> x = np.diag([1.+1.j]*2)
>>> x[1, 1] = 2 + 4.j
>>> x
array([[1.+1.j,  0.+0.j],
       [0.+0.j,  2.+4.j]])
>>> x.getfield(np.float64)
array([[1.,  0.],
       [0.,  2.]])

By choosing an offset of 8 bytes we can select the complex part of the array for our view:

>>> x.getfield(np.float64, offset=8)
array([[1.,  0.],
       [0.,  4.]])

heterodyne(self, phase, stride=1, singlesided=False)[source]¶

Compute the average magnitude and phase of this TimeSeries once per stride after heterodyning with a given phase series

Parameters

phase : array_like

an array of phase measurements (radians) with which to heterodyne the signal

stride : float, optional

stride (seconds) between calculations, defaults to 1 second

singlesided : bool, optional

Boolean switch to return single-sided output (i.e., to multiply by 2 so that the signal is distributed across positive frequencies only), default: False

Returns

out : TimeSeries

magnitude and phase trends, represented as mag * exp(1j*phase) with dt=stride

See also

TimeSeries.demodulate

for a method to heterodyne at a fixed frequency

Notes

This is similar to the demodulate() method, but is more general in that it accepts a varying phase evolution, rather than a fixed frequency.

Unlike demodulate(), the complex output is double-sided by default, so is not multiplied by 2.

Examples

Heterodyning can be useful in analysing quasi-monochromatic signals with a known phase evolution, such as continuous-wave signals from rapidly rotating neutron stars. These sources radiate at a frequency that slowly decreases over time, and is Doppler modulated due to the Earth’s rotational and orbital motion.

To see an example of heterodyning in action, we can simulate a signal whose phase evolution is described by the frequency and its first derivative with respect to time. We can download some O1 era LIGO-Livingston data from GWOSC, inject the simulated signal, and recover its amplitude.

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('L1', 1131350417, 1131354017)

We now need to set the signal parameters, generate the expected phase evolution, and create the signal:

>>> import numpy
>>> f0 = 123.456789  # signal frequency (Hz)
>>> fdot = -9.87654321e-7  # signal frequency derivative (Hz/s)
>>> fpeoch = 1131350417  # phase epoch
>>> amp = 1.5e-22  # signal amplitude
>>> phase0 = 0.4  # signal phase at the phase epoch
>>> times = data.times.value - fepoch
>>> phase = 2 * numpy.pi * (f0 * times + 0.5 * fdot * times**2)
>>> signal = TimeSeries(amp * numpy.cos(phase + phase0),
>>>                     sample_rate=data.sample_rate, t0=data.t0)
>>> data = data.inject(signal)

To recover the signal, we can bandpass the injected data around the signal frequency, then heterodyne using our phase model with a stride of 60 seconds:

>>> filtdata = data.bandpass(f0 - 0.5, f0 + 0.5)
>>> het = filtdata.heterodyne(phase, stride=60, singlesided=True)

We can then plot signal amplitude over time (cropping the first two minutes to remove the filter response):

>>> plot = het.crop(het.x0.value + 180).abs().plot()
>>> ax = plot.gca()
>>> ax.set_ylabel("Strain amplitude")
>>> plot.show()

highpass(self, frequency, gpass=2, gstop=30, fstop=None, type='iir', filtfilt=True, **kwargs)[source]¶

Filter this TimeSeries with a high-pass filter.

Parameters

frequency : float

high-pass corner frequency

gpass : float

the maximum loss in the passband (dB).

gstop : float

the minimum attenuation in the stopband (dB).

fstop : float

stop-band edge frequency, defaults to frequency * 1.5

type : str

the filter type, either 'iir' or 'fir'

**kwargs

other keyword arguments are passed to gwpy.signal.filter_design.highpass()

Returns

hpseries : TimeSeries

a high-passed version of the input TimeSeries

See also

gwpy.signal.filter_design.highpass

for details on the filter design

TimeSeries.filter

for details on how the filter is applied

Notes

When using scipy < 0.16.0 some higher-order filters may be unstable. With scipy >= 0.16.0 higher-order filters are decomposed into second-order-sections, and so are much more stable.

inject(self, other)[source]¶

Add two compatible Series along their shared x-axis values.

Parameters

other : Series

a Series whose xindex intersects with self.xindex

Returns

out : Series

the sum of self and other along their shared x-axis values

Raises

ValueError

if self and other have incompatible units or xindex intervals

Notes

If other.xindex and self.xindex do not intersect, this method will return a copy of self. If the series have uniformly offset indices, this method will raise a warning.

If self.xindex is an array of timestamps, and if other.xspan is not a subset of self.xspan, then other will be cropped before being adding to self.

Users who wish to taper or window their Series should do so before passing it to this method. See TimeSeries.taper() and planck() for more information.

insert(self, obj, values, axis=None)¶

Insert values along the given axis before the given indices and return a new Quantity object.

This is a thin wrapper around the numpy.insert function.

Parameters

obj : int, slice or sequence of ints

Object that defines the index or indices before which values is inserted.

values : array-like

Values to insert. If the type of values is different from that of quantity, values is converted to the matching type. values should be shaped so that it can be broadcast appropriately The unit of values must be consistent with this quantity.

axis : int, optional

Axis along which to insert values. If axis is None then the quantity array is flattened before insertion.

Returns

out : Quantity

A copy of quantity with values inserted. Note that the insertion does not occur in-place: a new quantity array is returned.

Examples

>>> import astropy.units as u
>>> q = [1, 2] * u.m
>>> q.insert(0, 50 * u.cm)
<Quantity [ 0.5,  1.,  2.] m>

>>> q = [[1, 2], [3, 4]] * u.m
>>> q.insert(1, [10, 20] * u.m, axis=0)
<Quantity [[  1.,  2.],
           [ 10., 20.],
           [  3.,  4.]] m>

>>> q.insert(1, 10 * u.m, axis=1)
<Quantity [[  1., 10.,  2.],
           [  3., 10.,  4.]] m>

is_compatible(self, other)[source]¶

Check whether this series and other have compatible metadata

This method tests that the sample size, and the unit match.

is_contiguous(self, other, tol=3.814697265625e-06)[source]¶

Check whether other is contiguous with self.

Parameters

other : Series, numpy.ndarray

another series of the same type to test for contiguity

tol : float, optional

the numerical tolerance of the test

Returns

1

if other is contiguous with this series, i.e. would attach seamlessly onto the end

-1

if other is anti-contiguous with this seires, i.e. would attach seamlessly onto the start

0

if other is completely dis-contiguous with thie series

Notes

if a raw numpy.ndarray is passed as other, with no metadata, then the contiguity check will always pass

item(*args)¶

Copy an element of an array to a standard Python scalar and return it.

Parameters

*args : Arguments (variable number and type)

• none: in this case, the method only works for arrays with one element (a.size == 1), which element is copied into a standard Python scalar object and returned.

• int_type: this argument is interpreted as a flat index into the array, specifying which element to copy and return.

• tuple of int_types: functions as does a single int_type argument, except that the argument is interpreted as an nd-index into the array.

Returns

z : Standard Python scalar object

A copy of the specified element of the array as a suitable Python scalar

Notes

When the data type of a is longdouble or clongdouble, item() returns a scalar array object because there is no available Python scalar that would not lose information. Void arrays return a buffer object for item(), unless fields are defined, in which case a tuple is returned.

item is very similar to a[args], except, instead of an array scalar, a standard Python scalar is returned. This can be useful for speeding up access to elements of the array and doing arithmetic on elements of the array using Python’s optimized math.

Examples

>>> np.random.seed(123)
>>> x = np.random.randint(9, size=(3, 3))
>>> x
array([[2, 2, 6],
       [1, 3, 6],
       [1, 0, 1]])
>>> x.item(3)
1
>>> x.item(7)
0
>>> x.item((0, 1))
2
>>> x.item((2, 2))
1

itemset(*args)¶

Insert scalar into an array (scalar is cast to array’s dtype, if possible)

There must be at least 1 argument, and define the last argument as item. Then, a.itemset(*args) is equivalent to but faster than a[args] = item. The item should be a scalar value and args must select a single item in the array a.

Parameters

*args : Arguments

If one argument: a scalar, only used in case a is of size 1. If two arguments: the last argument is the value to be set and must be a scalar, the first argument specifies a single array element location. It is either an int or a tuple.

Notes

Compared to indexing syntax, itemset provides some speed increase for placing a scalar into a particular location in an ndarray, if you must do this. However, generally this is discouraged: among other problems, it complicates the appearance of the code. Also, when using itemset (and item) inside a loop, be sure to assign the methods to a local variable to avoid the attribute look-up at each loop iteration.

Examples

>>> np.random.seed(123)
>>> x = np.random.randint(9, size=(3, 3))
>>> x
array([[2, 2, 6],
       [1, 3, 6],
       [1, 0, 1]])
>>> x.itemset(4, 0)
>>> x.itemset((2, 2), 9)
>>> x
array([[2, 2, 6],
       [1, 0, 6],
       [1, 0, 9]])

lowpass(self, frequency, gpass=2, gstop=30, fstop=None, type='iir', filtfilt=True, **kwargs)[source]¶

Filter this TimeSeries with a Butterworth low-pass filter.

Parameters

frequency : float

low-pass corner frequency

gpass : float

the maximum loss in the passband (dB).

gstop : float

the minimum attenuation in the stopband (dB).

fstop : float

stop-band edge frequency, defaults to frequency * 1.5

type : str

the filter type, either 'iir' or 'fir'

**kwargs

other keyword arguments are passed to gwpy.signal.filter_design.lowpass()

Returns

lpseries : TimeSeries

a low-passed version of the input TimeSeries

See also

gwpy.signal.filter_design.lowpass

for details on the filter design

TimeSeries.filter

for details on how the filter is applied

Notes

When using scipy < 0.16.0 some higher-order filters may be unstable. With scipy >= 0.16.0 higher-order filters are decomposed into second-order-sections, and so are much more stable.

max(axis=None, out=None, keepdims=False, initial=<no value>, where=True)¶

Return the maximum along a given axis.

Refer to numpy.amax for full documentation.

See also

numpy.amax

equivalent function

mean(axis=None, dtype=None, out=None, keepdims=False)¶

Returns the average of the array elements along given axis.

Refer to numpy.mean for full documentation.

See also

numpy.mean

equivalent function

median(self, axis=None, **kwargs)[source]¶

Compute the median along the specified axis.

Returns the median of the array elements.

Parameters

a : array_like

Input array or object that can be converted to an array.

axis : {int, sequence of int, None}, optional

Axis or axes along which the medians are computed. The default is to compute the median along a flattened version of the array. A sequence of axes is supported since version 1.9.0.

out : ndarray, optional

Alternative output array in which to place the result. It must have the same shape and buffer length as the expected output, but the type (of the output) will be cast if necessary.

overwrite_input : bool, optional

If True, then allow use of memory of input array a for calculations. The input array will be modified by the call to median. This will save memory when you do not need to preserve the contents of the input array. Treat the input as undefined, but it will probably be fully or partially sorted. Default is False. If overwrite_input is True and a is not already an ndarray, an error will be raised.

keepdims : bool, optional

If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original arr.

New in version 1.9.0.

Returns

median : ndarray

A new array holding the result. If the input contains integers or floats smaller than float64, then the output data-type is np.float64. Otherwise, the data-type of the output is the same as that of the input. If out is specified, that array is returned instead.

See also

mean, percentile

Notes

Given a vector V of length N, the median of V is the middle value of a sorted copy of V, V_sorted - i e., V_sorted[(N-1)/2], when N is odd, and the average of the two middle values of V_sorted when N is even.

Examples

>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10,  7,  4],
       [ 3,  2,  1]])
>>> np.median(a)
3.5
>>> np.median(a, axis=0)
array([6.5, 4.5, 2.5])
>>> np.median(a, axis=1)
array([7.,  2.])
>>> m = np.median(a, axis=0)
>>> out = np.zeros_like(m)
>>> np.median(a, axis=0, out=m)
array([6.5,  4.5,  2.5])
>>> m
array([6.5,  4.5,  2.5])
>>> b = a.copy()
>>> np.median(b, axis=1, overwrite_input=True)
array([7.,  2.])
>>> assert not np.all(a==b)
>>> b = a.copy()
>>> np.median(b, axis=None, overwrite_input=True)
3.5
>>> assert not np.all(a==b)

min(axis=None, out=None, keepdims=False, initial=<no value>, where=True)¶

Return the minimum along a given axis.

Refer to numpy.amin for full documentation.

See also

numpy.amin

equivalent function

nansum(self, axis=None, out=None, keepdims=False)¶

newbyteorder(new_order='S')¶

Return the array with the same data viewed with a different byte order.

Equivalent to:

arr.view(arr.dtype.newbytorder(new_order))

Changes are also made in all fields and sub-arrays of the array data type.

Parameters

new_order : string, optional

Byte order to force; a value from the byte order specifications below. new_order codes can be any of:

• ‘S’ - swap dtype from current to opposite endian

• {‘<’, ‘L’} - little endian

• {‘>’, ‘B’} - big endian

• {‘=’, ‘N’} - native order

• {‘|’, ‘I’} - ignore (no change to byte order)

The default value (‘S’) results in swapping the current byte order. The code does a case-insensitive check on the first letter of new_order for the alternatives above. For example, any of ‘B’ or ‘b’ or ‘biggish’ are valid to specify big-endian.

Returns

new_arr : array

New array object with the dtype reflecting given change to the byte order.

nonzero()¶

Return the indices of the elements that are non-zero.

Refer to numpy.nonzero for full documentation.

See also

numpy.nonzero

equivalent function

notch(self, frequency, type='iir', filtfilt=True, **kwargs)[source]¶

Notch out a frequency in this TimeSeries.

Parameters

frequency : float, Quantity

frequency (default in Hertz) at which to apply the notch

type : str, optional

type of filter to apply, currently only ‘iir’ is supported

**kwargs

other keyword arguments to pass to scipy.signal.iirdesign

Returns

notched : TimeSeries

a notch-filtered copy of the input TimeSeries

See also

TimeSeries.filter

for details on the filtering method

scipy.signal.iirdesign

for details on the IIR filter design method

override_unit(self, unit, parse_strict='raise')[source]¶

Forcefully reset the unit of these data

Use of this method is discouraged in favour of to(), which performs accurate conversions from one unit to another. The method should really only be used when the original unit of the array is plain wrong.

Parameters

unit : Unit, str

the unit to force onto this array

parse_strict : str, optional

how to handle errors in the unit parsing, default is to raise the underlying exception from astropy.units

Raises

ValueError

if a str cannot be parsed as a valid unit

pad(self, pad_width, **kwargs)[source]¶

Pad this series to a new size

Parameters

pad_width : int, pair of ints

number of samples by which to pad each end of the array. Single int to pad both ends by the same amount, or (before, after) tuple to give uneven padding

**kwargs

see numpy.pad() for kwarg documentation

Returns

series : Series

the padded version of the input

See also

numpy.pad

for details on the underlying functionality

partition(kth, axis=-1, kind='introselect', order=None)¶

Rearranges the elements in the array in such a way that the value of the element in kth position is in the position it would be in a sorted array. All elements smaller than the kth element are moved before this element and all equal or greater are moved behind it. The ordering of the elements in the two partitions is undefined.

New in version 1.8.0.

Parameters

kth : int or sequence of ints

Element index to partition by. The kth element value will be in its final sorted position and all smaller elements will be moved before it and all equal or greater elements behind it. The order of all elements in the partitions is undefined. If provided with a sequence of kth it will partition all elements indexed by kth of them into their sorted position at once.

axis : int, optional

Axis along which to sort. Default is -1, which means sort along the last axis.

kind : {‘introselect’}, optional

Selection algorithm. Default is ‘introselect’.

order : str or list of str, optional

When a is an array with fields defined, this argument specifies which fields to compare first, second, etc. A single field can be specified as a string, and not all fields need to be specified, but unspecified fields will still be used, in the order in which they come up in the dtype, to break ties.

See also

numpy.partition

Return a parititioned copy of an array.

argpartition

Indirect partition.

sort

Full sort.

Notes

See np.partition for notes on the different algorithms.

Examples

>>> a = np.array([3, 4, 2, 1])
>>> a.partition(3)
>>> a
array([2, 1, 3, 4])

>>> a.partition((1, 3))
>>> a
array([1, 2, 3, 4])

plot(self, method='plot', figsize=(12, 4), xscale='auto-gps', **kwargs)[source]¶

Plot the data for this timeseries

Returns

figure : Figure

the newly created figure, with populated Axes.

See also

matplotlib.pyplot.figure

for documentation of keyword arguments used to create the figure

matplotlib.figure.Figure.add_subplot

for documentation of keyword arguments used to create the axes

matplotlib.axes.Axes.plot

for documentation of keyword arguments used in rendering the data

prepend(self, other, inplace=True, pad=None, gap=None, resize=True)[source]¶

Connect another series onto the start of the current one.

Parameters

other : Series

another series of the same type as this one

inplace : bool, optional

perform operation in-place, modifying current series, otherwise copy data and return new series, default: True

Warning

inplace prepend bypasses the reference check in numpy.ndarray.resize, so be carefully to only use this for arrays that haven’t been sharing their memory!

pad : float, optional

value with which to pad discontiguous series, by default gaps will result in a ValueError.

gap : str, optional

action to perform if there’s a gap between the other series and this one. One of

• 'raise' - raise a ValueError

• 'ignore' - remove gap and join data

• 'pad' - pad gap with zeros

If pad is given and is not None, the default is 'pad', otherwise 'raise'.

resize : bool, optional

resize this array to accommodate new data, otherwise shift the old data to the left (potentially falling off the start) and put the new data in at the end, default: True.

Returns

series : TimeSeries

time-series containing joined data sets

prod(axis=None, dtype=None, out=None, keepdims=False, initial=1, where=True)¶

Return the product of the array elements over the given axis

Refer to numpy.prod for full documentation.

See also

numpy.prod

equivalent function

psd(self, fftlength=None, overlap=None, window='hann', method='welch', **kwargs)[source]¶

Calculate the PSD FrequencySeries for this TimeSeries

Parameters

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

method : str, optional

FFT-averaging method, see Notes for more details

**kwargs

other keyword arguments are passed to the underlying PSD-generation method

Returns

psd : FrequencySeries

a data series containing the PSD.

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

ptp(axis=None, out=None, keepdims=False)¶

Peak to peak (maximum - minimum) value along a given axis.

Refer to numpy.ptp for full documentation.

See also

numpy.ptp

equivalent function

put(indices, values, mode='raise')¶

Set a.flat[n] = values[n] for all n in indices.

Refer to numpy.put for full documentation.

See also

numpy.put

equivalent function

q_gram(self, qrange=(4, 64), frange=(0, inf), mismatch=0.2, snrthresh=5.5, **kwargs)[source]¶

Scan a TimeSeries using the multi-Q transform and return an EventTable of the most significant tiles

Parameters

qrange : tuple of float, optional

(low, high) range of Qs to scan

frange : tuple of float, optional

(low, high) range of frequencies to scan

mismatch : float, optional

maximum allowed fractional mismatch between neighbouring tiles

snrthresh : float, optional

lower inclusive threshold on individual tile SNR to keep in the table

**kwargs

other keyword arguments to be passed to QTiling.transform(), including 'epoch' and 'search'

Returns

qgram : EventTable

a table of time-frequency tiles on the most significant QPlane

See also

TimeSeries.q_transform

for a method to interpolate the raw Q-transform over a regularly gridded spectrogram

gwpy.signal.qtransform

for code and documentation on how the Q-transform is implemented

gwpy.table.EventTable.tile

to render this EventTable as a collection of polygons

Notes

Only tiles with signal energy greater than or equal to snrthresh ** 2 / 2 will be stored in the output EventTable. The table columns are 'time', 'duration', 'frequency', 'bandwidth', and 'energy'.

q_transform(self, qrange=(4, 64), frange=(0, inf), gps=None, search=0.5, tres='<default>', fres='<default>', logf=False, norm='median', mismatch=0.2, outseg=None, whiten=True, fduration=2, highpass=None, **asd_kw)[source]¶

Scan a TimeSeries using the multi-Q transform and return an interpolated high-resolution spectrogram

By default, this method returns a high-resolution spectrogram in both time and frequency, which can result in a large memory footprint. If you know that you only need a subset of the output for, say, a figure, consider using outseg and the other keyword arguments to restrict the size of the returned data.

Parameters

qrange : tuple of float, optional

(low, high) range of Qs to scan

frange : tuple of float, optional

(log, high) range of frequencies to scan

gps : float, optional

central time of interest for determine loudest Q-plane

search : float, optional

window around gps in which to find peak energies, only used if gps is given

tres : float, optional

desired time resolution (seconds) of output Spectrogram, default is abs(outseg) / 1000.

fres : float, int, None, optional

desired frequency resolution (Hertz) of output Spectrogram, or, if logf=True, the number of frequency samples; give None to skip this step and return the original resolution, default is 0.5 Hz or 500 frequency samples

logf : bool, optional

boolean switch to enable (True) or disable (False) use of log-sampled frequencies in the output Spectrogram, if True then fres is interpreted as a number of frequency samples, default: False

norm : bool, str, optional

whether to normalize the returned Q-transform output, or how, default: True ('median'), other options: False, 'mean'

mismatch : float

maximum allowed fractional mismatch between neighbouring tiles

outseg : Segment, optional

GPS [start, stop) segment for output Spectrogram, default is the full duration of the input

whiten : bool, FrequencySeries, optional

boolean switch to enable (True) or disable (False) data whitening, or an ASD FrequencySeries with which to whiten the data

fduration : float, optional

duration (in seconds) of the time-domain FIR whitening filter, only used if whiten is not False, defaults to 2 seconds

highpass : float, optional

highpass corner frequency (in Hz) of the FIR whitening filter, used only if whiten is not False, default: None

**asd_kw

keyword arguments to pass to TimeSeries.asd to generate an ASD to use when whitening the data

Returns

out : Spectrogram

output Spectrogram of normalised Q energy

See also

TimeSeries.asd

for documentation on acceptable **asd_kw

TimeSeries.whiten

for documentation on how the whitening is done

gwpy.signal.qtransform

for code and documentation on how the Q-transform is implemented

Notes

This method will return a Spectrogram of dtype float32 if norm is given, and float64 otherwise.

To optimize plot rendering with pcolormesh, the output Spectrogram can be given a log-sampled frequency axis by passing logf=True at runtime. The fres argument is then the number of points on the frequency axis. Note, this is incompatible with imshow.

It is also highly recommended to use the outseg keyword argument when only a small window around a given GPS time is of interest. This will speed up this method a little, but can greatly speed up rendering the resulting Spectrogram using pcolormesh.

If you aren’t going to use pcolormesh in the end, don’t worry.

Examples

>>> from numpy.random import normal
>>> from scipy.signal import gausspulse
>>> from gwpy.timeseries import TimeSeries

Generate a TimeSeries containing Gaussian noise sampled at 4096 Hz, centred on GPS time 0, with a sine-Gaussian pulse (‘glitch’) at 500 Hz:

>>> noise = TimeSeries(normal(loc=1, size=4096*4), sample_rate=4096, epoch=-2)
>>> glitch = TimeSeries(gausspulse(noise.times.value, fc=500) * 4, sample_rate=4096)
>>> data = noise + glitch

Compute and plot the Q-transform of these data:

>>> q = data.q_transform()
>>> plot = q.plot()
>>> ax = plot.gca()
>>> ax.set_xlim(-.2, .2)
>>> ax.set_epoch(0)
>>> plot.show()

(png)

ravel([order])¶

Return a flattened array.

Refer to numpy.ravel for full documentation.

See also

numpy.ravel

equivalent function

ndarray.flat

a flat iterator on the array.

rayleigh_spectrogram(self, stride, fftlength=None, overlap=0, nproc=1, **kwargs)[source]¶

Calculate the Rayleigh statistic spectrogram of this TimeSeries

Parameters

stride : float

number of seconds in single PSD (column of spectrogram).

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, default: 0

nproc : int, optional

maximum number of independent frame reading processes, default default: 1

Returns

spectrogram : Spectrogram

time-frequency Rayleigh spectrogram as generated from the input time-series.

See also

TimeSeries.rayleigh

for details of the statistic calculation

rayleigh_spectrum(self, fftlength=None, overlap=None)[source]¶

Calculate the Rayleigh FrequencySeries for this TimeSeries.

The Rayleigh statistic is calculated as the ratio of the standard deviation and the mean of a number of periodograms.

Parameters

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to that of the relevant method.

Returns

psd : FrequencySeries

a data series containing the PSD.

classmethod read(source, *args, **kwargs)[source]¶

Read data into a TimeSeries

Arguments and keywords depend on the output format, see the online documentation for full details for each format, the parameters below are common to most formats.

Parameters

source : str, list

Source of data, any of the following:

• str path of single data file,

• str path of LAL-format cache file,

• list of paths.

name : str, Channel

the name of the channel to read, or a Channel object.

start : LIGOTimeGPS, float, str, optional

GPS start time of required data, defaults to start of data found; any input parseable by to_gps is fine

end : LIGOTimeGPS, float, str, optional

GPS end time of required data, defaults to end of data found; any input parseable by to_gps is fine

format : str, optional

source format identifier. If not given, the format will be detected if possible. See below for list of acceptable formats.

nproc : int, optional

number of parallel processes to use, serial process by default.

pad : float, optional

value with which to fill gaps in the source data, by default gaps will result in a ValueError.

Raises

IndexError

if source is an empty list

Notes

The available built-in formats are:

Format	Read	Write	Auto-identify
csv	Yes	Yes	Yes
gwf	Yes	Yes	Yes
gwf.framecpp	Yes	Yes	No
gwf.lalframe	Yes	Yes	No
hdf5	Yes	Yes	Yes
hdf5.losc	Yes	No	No
txt	Yes	Yes	Yes
wav	Yes	No	No

repeat(repeats, axis=None)¶

Repeat elements of an array.

Refer to numpy.repeat for full documentation.

See also

numpy.repeat

equivalent function

resample(self, rate, window='hamming', ftype='fir', n=None)[source]¶

Resample this Series to a new rate

Parameters

rate : float

rate to which to resample this Series

window : str, numpy.ndarray, optional

window function to apply to signal in the Fourier domain, see scipy.signal.get_window() for details on acceptable formats, only used for ftype='fir' or irregular downsampling

ftype : str, optional

type of filter, either ‘fir’ or ‘iir’, defaults to ‘fir’

n : int, optional

if ftype='fir' the number of taps in the filter, otherwise the order of the Chebyshev type I IIR filter

Returns

Series

a new Series with the resampling applied, and the same metadata

reshape(shape, order='C')¶

Returns an array containing the same data with a new shape.

Refer to numpy.reshape for full documentation.

See also

numpy.reshape

equivalent function

Notes

Unlike the free function numpy.reshape, this method on ndarray allows the elements of the shape parameter to be passed in as separate arguments. For example, a.reshape(10, 11) is equivalent to a.reshape((10, 11)).

resize(new_shape, refcheck=True)¶

Change shape and size of array in-place.

Parameters

new_shape : tuple of ints, or n ints

Shape of resized array.

refcheck : bool, optional

If False, reference count will not be checked. Default is True.

Returns

None

Raises

ValueError

If a does not own its own data or references or views to it exist, and the data memory must be changed. PyPy only: will always raise if the data memory must be changed, since there is no reliable way to determine if references or views to it exist.

SystemError

If the order keyword argument is specified. This behaviour is a bug in NumPy.

See also

resize

Return a new array with the specified shape.

Notes

This reallocates space for the data area if necessary.

Only contiguous arrays (data elements consecutive in memory) can be resized.

The purpose of the reference count check is to make sure you do not use this array as a buffer for another Python object and then reallocate the memory. However, reference counts can increase in other ways so if you are sure that you have not shared the memory for this array with another Python object, then you may safely set refcheck to False.

Examples

Shrinking an array: array is flattened (in the order that the data are stored in memory), resized, and reshaped:

>>> a = np.array([[0, 1], [2, 3]], order='C')
>>> a.resize((2, 1))
>>> a
array([[0],
       [1]])

>>> a = np.array([[0, 1], [2, 3]], order='F')
>>> a.resize((2, 1))
>>> a
array([[0],
       [2]])

Enlarging an array: as above, but missing entries are filled with zeros:

>>> b = np.array([[0, 1], [2, 3]])
>>> b.resize(2, 3) # new_shape parameter doesn't have to be a tuple
>>> b
array([[0, 1, 2],
       [3, 0, 0]])

Referencing an array prevents resizing…

>>> c = a
>>> a.resize((1, 1))
Traceback (most recent call last):
...
ValueError: cannot resize an array that references or is referenced ...

Unless refcheck is False:

>>> a.resize((1, 1), refcheck=False)
>>> a
array([[0]])
>>> c
array([[0]])

rms(self, stride=1)[source]¶

Calculate the root-mean-square value of this TimeSeries once per stride.

Parameters

stride : float

stride (seconds) between RMS calculations

Returns

rms : TimeSeries

a new TimeSeries containing the RMS value with dt=stride

round(decimals=0, out=None)¶

Return a with each element rounded to the given number of decimals.

Refer to numpy.around for full documentation.

See also

numpy.around

equivalent function

searchsorted(v, side='left', sorter=None)¶

Find indices where elements of v should be inserted in a to maintain order.

For full documentation, see numpy.searchsorted

See also

numpy.searchsorted

equivalent function

setfield(val, dtype, offset=0)¶

Put a value into a specified place in a field defined by a data-type.

Place val into a’s field defined by dtype and beginning offset bytes into the field.

Parameters

val : object

Value to be placed in field.

dtype : dtype object

Data-type of the field in which to place val.

offset : int, optional

The number of bytes into the field at which to place val.

Returns

None

See also

getfield

Examples

>>> x = np.eye(3)
>>> x.getfield(np.float64)
array([[1.,  0.,  0.],
       [0.,  1.,  0.],
       [0.,  0.,  1.]])
>>> x.setfield(3, np.int32)
>>> x.getfield(np.int32)
array([[3, 3, 3],
       [3, 3, 3],
       [3, 3, 3]], dtype=int32)
>>> x
array([[1.0e+000, 1.5e-323, 1.5e-323],
       [1.5e-323, 1.0e+000, 1.5e-323],
       [1.5e-323, 1.5e-323, 1.0e+000]])
>>> x.setfield(np.eye(3), np.int32)
>>> x
array([[1.,  0.,  0.],
       [0.,  1.,  0.],
       [0.,  0.,  1.]])

setflags(write=None, align=None, uic=None)¶

Set array flags WRITEABLE, ALIGNED, (WRITEBACKIFCOPY and UPDATEIFCOPY), respectively.

These Boolean-valued flags affect how numpy interprets the memory area used by a (see Notes below). The ALIGNED flag can only be set to True if the data is actually aligned according to the type. The WRITEBACKIFCOPY and (deprecated) UPDATEIFCOPY flags can never be set to True. The flag WRITEABLE can only be set to True if the array owns its own memory, or the ultimate owner of the memory exposes a writeable buffer interface, or is a string. (The exception for string is made so that unpickling can be done without copying memory.)

Parameters

write : bool, optional

Describes whether or not a can be written to.

align : bool, optional

Describes whether or not a is aligned properly for its type.

uic : bool, optional

Describes whether or not a is a copy of another “base” array.

Notes

Array flags provide information about how the memory area used for the array is to be interpreted. There are 7 Boolean flags in use, only four of which can be changed by the user: WRITEBACKIFCOPY, UPDATEIFCOPY, WRITEABLE, and ALIGNED.

WRITEABLE (W) the data area can be written to;

ALIGNED (A) the data and strides are aligned appropriately for the hardware (as determined by the compiler);

UPDATEIFCOPY (U) (deprecated), replaced by WRITEBACKIFCOPY;

WRITEBACKIFCOPY (X) this array is a copy of some other array (referenced by .base). When the C-API function PyArray_ResolveWritebackIfCopy is called, the base array will be updated with the contents of this array.

All flags can be accessed using the single (upper case) letter as well as the full name.

Examples

>>> y = np.array([[3, 1, 7],
...               [2, 0, 0],
...               [8, 5, 9]])
>>> y
array([[3, 1, 7],
       [2, 0, 0],
       [8, 5, 9]])
>>> y.flags
  C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False
>>> y.setflags(write=0, align=0)
>>> y.flags
  C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  WRITEABLE : False
  ALIGNED : False
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False
>>> y.setflags(uic=1)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: cannot set WRITEBACKIFCOPY flag to True

shift(self, delta)[source]¶

Shift this Series forward on the X-axis by delta

This modifies the series in-place.

Parameters

delta : float, Quantity, str

The amount by which to shift (in x-axis units if float), give a negative value to shift backwards in time

Examples

>>> from gwpy.types import Series
>>> a = Series([1, 2, 3, 4, 5], x0=0, dx=1, xunit='m')
>>> print(a.x0)
0.0 m
>>> a.shift(5)
>>> print(a.x0)
5.0 m
>>> a.shift('-1 km')
-995.0 m

sort(axis=-1, kind=None, order=None)¶

Sort an array in-place. Refer to numpy.sort for full documentation.

Parameters

axis : int, optional

Axis along which to sort. Default is -1, which means sort along the last axis.

kind : {‘quicksort’, ‘mergesort’, ‘heapsort’, ‘stable’}, optional

Sorting algorithm. The default is ‘quicksort’. Note that both ‘stable’ and ‘mergesort’ use timsort under the covers and, in general, the actual implementation will vary with datatype. The ‘mergesort’ option is retained for backwards compatibility.

Changed in version 1.15.0.: The ‘stable’ option was added.

order : str or list of str, optional

When a is an array with fields defined, this argument specifies which fields to compare first, second, etc. A single field can be specified as a string, and not all fields need be specified, but unspecified fields will still be used, in the order in which they come up in the dtype, to break ties.

See also

numpy.sort

Return a sorted copy of an array.

argsort

Indirect sort.

lexsort

Indirect stable sort on multiple keys.

searchsorted

Find elements in sorted array.

partition

Partial sort.

Notes

See numpy.sort for notes on the different sorting algorithms.

Examples

>>> a = np.array([[1,4], [3,1]])
>>> a.sort(axis=1)
>>> a
array([[1, 4],
       [1, 3]])
>>> a.sort(axis=0)
>>> a
array([[1, 3],
       [1, 4]])

Use the order keyword to specify a field to use when sorting a structured array:

>>> a = np.array([('a', 2), ('c', 1)], dtype=[('x', 'S1'), ('y', int)])
>>> a.sort(order='y')
>>> a
array([(b'c', 1), (b'a', 2)],
      dtype=[('x', 'S1'), ('y', '<i8')])

spectral_variance(self, stride, fftlength=None, overlap=None, method='welch', window='hann', nproc=1, filter=None, bins=None, low=None, high=None, nbins=500, log=False, norm=False, density=False)[source]¶

Calculate the SpectralVariance of this TimeSeries.

Parameters

stride : float

number of seconds in single PSD (column of spectrogram)

fftlength : float

number of seconds in single FFT

method : str, optional

FFT-averaging method, see Notes for more details

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

nproc : int

maximum number of independent frame reading processes, default is set to single-process file reading.

bins : numpy.ndarray, optional, default None

array of histogram bin edges, including the rightmost edge

low : float, optional

left edge of lowest amplitude bin, only read if bins is not given

high : float, optional

right edge of highest amplitude bin, only read if bins is not given

nbins : int, optional

number of bins to generate, only read if bins is not given

log : bool, optional

calculate amplitude bins over a logarithmic scale, only read if bins is not given

norm : bool, optional

normalise bin counts to a unit sum

density : bool, optional

normalise bin counts to a unit integral

Returns

specvar : SpectralVariance

2D-array of spectral frequency-amplitude counts

See also

numpy.histogram

for details on specifying bins and weights

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

spectrogram(self, stride, fftlength=None, overlap=None, window='hann', method='welch', nproc=1, **kwargs)[source]¶

Calculate the average power spectrogram of this TimeSeries using the specified average spectrum method.

Each time-bin of the output Spectrogram is calculated by taking a chunk of the TimeSeries in the segment [t - overlap/2., t + stride + overlap/2.) and calculating the psd() of those data.

As a result, each time-bin is calculated using stride + overlap seconds of data.

Parameters

stride : float

number of seconds in single PSD (column of spectrogram).

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

method : str, optional

FFT-averaging method, see Notes for more details

nproc : int

number of CPUs to use in parallel processing of FFTs

Returns

spectrogram : Spectrogram

time-frequency power spectrogram as generated from the input time-series.

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

spectrogram2(self, fftlength, overlap=None, window='hann', **kwargs)[source]¶

Calculate the non-averaged power Spectrogram of this TimeSeries

Parameters

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

scaling : [ ‘density’ | ‘spectrum’ ], optional

selects between computing the power spectral density (‘density’) where the Spectrogram has units of V**2/Hz if the input is measured in V and computing the power spectrum (‘spectrum’) where the Spectrogram has units of V**2 if the input is measured in V. Defaults to ‘density’.

**kwargs

other parameters to be passed to scipy.signal.periodogram for each column of the Spectrogram

Returns

spectrogram: Spectrogram

a power Spectrogram with 1/fftlength frequency resolution and (fftlength - overlap) time resolution.

See also

scipy.signal.periodogram

for documentation on the Fourier methods used in this calculation

Notes

This method calculates overlapping periodograms for all possible chunks of data entirely containing within the span of the input TimeSeries, then normalises the power in overlapping chunks using a triangular window centred on that chunk which most overlaps the given Spectrogram time sample.

squeeze(axis=None)¶

Remove single-dimensional entries from the shape of a.

Refer to numpy.squeeze for full documentation.

See also

numpy.squeeze

equivalent function

std(axis=None, dtype=None, out=None, ddof=0, keepdims=False)¶

Returns the standard deviation of the array elements along given axis.

Refer to numpy.std for full documentation.

See also

numpy.std

equivalent function

step(self, **kwargs)[source]¶

Create a step plot of this series

sum(axis=None, dtype=None, out=None, keepdims=False, initial=0, where=True)¶

Return the sum of the array elements over the given axis.

Refer to numpy.sum for full documentation.

See also

numpy.sum

equivalent function

swapaxes(axis1, axis2)¶

Return a view of the array with axis1 and axis2 interchanged.

Refer to numpy.swapaxes for full documentation.

See also

numpy.swapaxes

equivalent function

take(indices, axis=None, out=None, mode='raise')¶

Return an array formed from the elements of a at the given indices.

Refer to numpy.take for full documentation.

See also

numpy.take

equivalent function

taper(self, side='leftright', duration=None, nsamples=None)[source]¶

Taper the ends of this TimeSeries smoothly to zero.

Parameters

side : str, optional

the side of the TimeSeries to taper, must be one of 'left', 'right', or 'leftright'

duration : float, optional

the duration of time to taper, will override nsamples if both are provided as arguments

nsamples : int, optional

the number of samples to taper, will be overridden by duration if both are provided as arguments

Returns

out : TimeSeries

a copy of self tapered at one or both ends

Raises

ValueError

if side is not one of ('left', 'right', 'leftright')

Notes

The TimeSeries.taper() automatically tapers from the second stationary point (local maximum or minimum) on the specified side of the input. However, the method will never taper more than half the full width of the TimeSeries, and will fail if there are no stationary points.

See planck() for the generic Planck taper window, and see scipy.signal.get_window() for other common window formats.

Examples

To see the effect of the Planck-taper window, we can taper a sinusoidal TimeSeries at both ends:

>>> import numpy
>>> from gwpy.timeseries import TimeSeries
>>> t = numpy.linspace(0, 1, 2048)
>>> series = TimeSeries(numpy.cos(10.5*numpy.pi*t), times=t)
>>> tapered = series.taper()

We can plot it to see how the ends now vary smoothly from 0 to 1:

>>> from gwpy.plot import Plot
>>> plot = Plot(series, tapered, separate=True, sharex=True)
>>> plot.show()

(png)

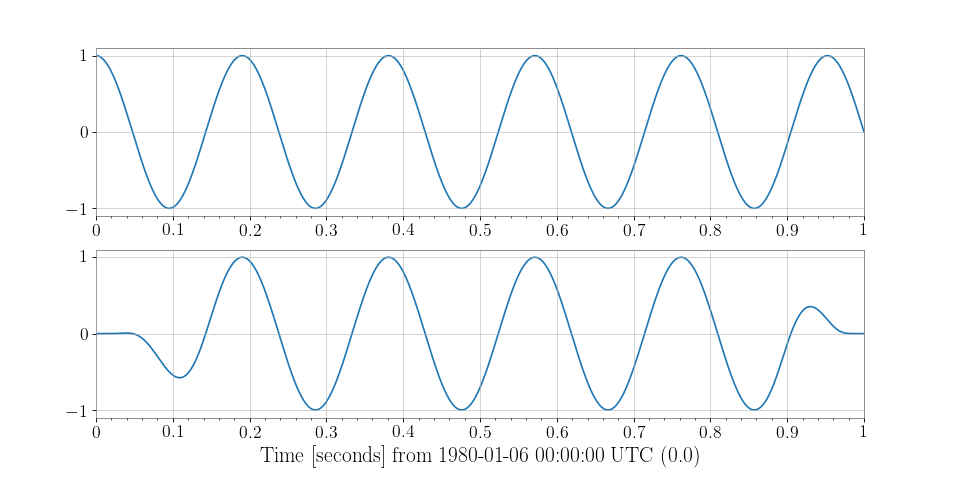
to(self, unit, equivalencies=[])¶

Return a new Quantity object with the specified unit.

Parameters

unit : UnitBase instance, str

An object that represents the unit to convert to. Must be an UnitBase object or a string parseable by the units package.

equivalencies : list of equivalence pairs, optional

A list of equivalence pairs to try if the units are not directly convertible. See Equivalencies. If not provided or [], class default equivalencies will be used (none for Quantity, but may be set for subclasses) If None, no equivalencies will be applied at all, not even any set globally or within a context.

See also

to_value

get the numerical value in a given unit.

to_lal(self)[source]¶

Convert this TimeSeries into a LAL TimeSeries.

to_pycbc(self, copy=True)[source]¶

Convert this TimeSeries into a PyCBC TimeSeries

Parameters

copy : bool, optional, default: True

if True, copy these data to a new array

Returns

timeseries : TimeSeries

a PyCBC representation of this TimeSeries

to_string(self, unit=None, precision=None, format=None, subfmt=None)¶

Generate a string representation of the quantity and its unit.

The behavior of this function can be altered via the numpy.set_printoptions function and its various keywords. The exception to this is the threshold keyword, which is controlled via the [units.quantity] configuration item latex_array_threshold. This is treated separately because the numpy default of 1000 is too big for most browsers to handle.

Parameters

unit : UnitBase, optional

Specifies the unit. If not provided, the unit used to initialize the quantity will be used.

precision : numeric, optional

The level of decimal precision. If None, or not provided, it will be determined from NumPy print options.

format : str, optional

The format of the result. If not provided, an unadorned string is returned. Supported values are:

• ‘latex’: Return a LaTeX-formatted string

subfmt : str, optional

Subformat of the result. For the moment, only used for format=”latex”. Supported values are:

• ‘inline’: Use $ ... $ as delimiters.

• ‘display’: Use $\displaystyle ... $ as delimiters.

Returns

lstr

A string with the contents of this Quantity

to_value(self, unit=None, equivalencies=[])¶

The numerical value, possibly in a different unit.

Parameters

unit : UnitBase instance or str, optional

The unit in which the value should be given. If not given or None, use the current unit.

equivalencies : list of equivalence pairs, optional

A list of equivalence pairs to try if the units are not directly convertible (see Equivalencies). If not provided or [], class default equivalencies will be used (none for Quantity, but may be set for subclasses). If None, no equivalencies will be applied at all, not even any set globally or within a context.

Returns

value : ndarray or scalar

The value in the units specified. For arrays, this will be a view of the data if no unit conversion was necessary.

See also

to

Get a new instance in a different unit.

tobytes(order='C')¶

Construct Python bytes containing the raw data bytes in the array.

Constructs Python bytes showing a copy of the raw contents of data memory. The bytes object can be produced in either ‘C’ or ‘Fortran’, or ‘Any’ order (the default is ‘C’-order). ‘Any’ order means C-order unless the F_CONTIGUOUS flag in the array is set, in which case it means ‘Fortran’ order.

New in version 1.9.0.

Parameters

order : {‘C’, ‘F’, None}, optional

Order of the data for multidimensional arrays: C, Fortran, or the same as for the original array.

Returns

s : bytes

Python bytes exhibiting a copy of a’s raw data.

Examples

>>> x = np.array([[0, 1], [2, 3]], dtype='<u2')
>>> x.tobytes()
b'\x00\x00\x01\x00\x02\x00\x03\x00'
>>> x.tobytes('C') == x.tobytes()
True
>>> x.tobytes('F')
b'\x00\x00\x02\x00\x01\x00\x03\x00'

tofile(fid, sep="", format="%s")¶

Write array to a file as text or binary (default).

Data is always written in ‘C’ order, independent of the order of a. The data produced by this method can be recovered using the function fromfile().

Parameters

fid : file or str or Path

An open file object, or a string containing a filename.

Changed in version 1.17.0: pathlib.Path objects are now accepted.

sep : str

Separator between array items for text output. If “” (empty), a binary file is written, equivalent to file.write(a.tobytes()).

format : str

Format string for text file output. Each entry in the array is formatted to text by first converting it to the closest Python type, and then using “format” % item.

Notes

This is a convenience function for quick storage of array data. Information on endianness and precision is lost, so this method is not a good choice for files intended to archive data or transport data between machines with different endianness. Some of these problems can be overcome by outputting the data as text files, at the expense of speed and file size.

When fid is a file object, array contents are directly written to the file, bypassing the file object’s write method. As a result, tofile cannot be used with files objects supporting compression (e.g., GzipFile) or file-like objects that do not support fileno() (e.g., BytesIO).

tolist()¶

Return the array as an a.ndim-levels deep nested list of Python scalars.

Return a copy of the array data as a (nested) Python list. Data items are converted to the nearest compatible builtin Python type, via the item function.

If a.ndim is 0, then since the depth of the nested list is 0, it will not be a list at all, but a simple Python scalar.

Parameters

none

Returns

y : object, or list of object, or list of list of object, or …

The possibly nested list of array elements.

Notes

The array may be recreated via a = np.array(a.tolist()), although this may sometimes lose precision.

Examples

For a 1D array, a.tolist() is almost the same as list(a):

>>> a = np.array([1, 2])
>>> list(a)
[1, 2]
>>> a.tolist()
[1, 2]

However, for a 2D array, tolist applies recursively:

>>> a = np.array([[1, 2], [3, 4]])
>>> list(a)
[array([1, 2]), array([3, 4])]
>>> a.tolist()
[[1, 2], [3, 4]]

The base case for this recursion is a 0D array:

>>> a = np.array(1)
>>> list(a)
Traceback (most recent call last):
  ...
TypeError: iteration over a 0-d array
>>> a.tolist()
1

tostring(order='C')[source]¶

Construct Python bytes containing the raw data bytes in the array.

Constructs Python bytes showing a copy of the raw contents of data memory. The bytes object can be produced in either ‘C’ or ‘Fortran’, or ‘Any’ order (the default is ‘C’-order). ‘Any’ order means C-order unless the F_CONTIGUOUS flag in the array is set, in which case it means ‘Fortran’ order.

This function is a compatibility alias for tobytes. Despite its name it returns bytes not strings.

Parameters

order : {‘C’, ‘F’, None}, optional

Order of the data for multidimensional arrays: C, Fortran, or the same as for the original array.

Returns

s : bytes

Python bytes exhibiting a copy of a’s raw data.

Examples

>>> x = np.array([[0, 1], [2, 3]], dtype='<u2')
>>> x.tobytes()
b'\x00\x00\x01\x00\x02\x00\x03\x00'
>>> x.tobytes('C') == x.tobytes()
True
>>> x.tobytes('F')
b'\x00\x00\x02\x00\x01\x00\x03\x00'

trace(offset=0, axis1=0, axis2=1, dtype=None, out=None)¶

Return the sum along diagonals of the array.

Refer to numpy.trace for full documentation.

See also

numpy.trace

equivalent function

transpose(*axes)¶

Returns a view of the array with axes transposed.

For a 1-D array this has no effect, as a transposed vector is simply the same vector. To convert a 1-D array into a 2D column vector, an additional dimension must be added. np.atleast2d(a).T achieves this, as does a[:, np.newaxis]. For a 2-D array, this is a standard matrix transpose. For an n-D array, if axes are given, their order indicates how the axes are permuted (see Examples). If axes are not provided and a.shape = (i[0], i[1], ... i[n-2], i[n-1]), then a.transpose().shape = (i[n-1], i[n-2], ... i[1], i[0]).

Parameters

axes : None, tuple of ints, or n ints

• None or no argument: reverses the order of the axes.

• tuple of ints: i in the j-th place in the tuple means a’s i-th axis becomes a.transpose()’s j-th axis.

• n ints: same as an n-tuple of the same ints (this form is intended simply as a “convenience” alternative to the tuple form)

Returns

out : ndarray

View of a, with axes suitably permuted.

See also

ndarray.T

Array property returning the array transposed.

ndarray.reshape

Give a new shape to an array without changing its data.

Examples

>>> a = np.array([[1, 2], [3, 4]])
>>> a
array([[1, 2],
       [3, 4]])
>>> a.transpose()
array([[1, 3],
       [2, 4]])
>>> a.transpose((1, 0))
array([[1, 3],
       [2, 4]])
>>> a.transpose(1, 0)
array([[1, 3],
       [2, 4]])

update(self, other, inplace=True)[source]¶

Update this series by appending new data from an other and dropping the same amount of data off the start.

This is a convenience method that just calls append with resize=False.

value_at(self, x)[source]¶

Return the value of this Series at the given xindex value

Parameters

x : float, Quantity

the xindex value at which to search

Returns

y : Quantity

the value of this Series at the given xindex value

var(axis=None, dtype=None, out=None, ddof=0, keepdims=False)¶

Returns the variance of the array elements, along given axis.

Refer to numpy.var for full documentation.

See also

numpy.var

equivalent function

view(dtype=None, type=None)¶

New view of array with the same data.

Parameters

dtype : data-type or ndarray sub-class, optional

Data-type descriptor of the returned view, e.g., float32 or int16. The default, None, results in the view having the same data-type as a. This argument can also be specified as an ndarray sub-class, which then specifies the type of the returned object (this is equivalent to setting the type parameter).

type : Python type, optional

Type of the returned view, e.g., ndarray or matrix. Again, the default None results in type preservation.

Notes

a.view() is used two different ways:

a.view(some_dtype) or a.view(dtype=some_dtype) constructs a view of the array’s memory with a different data-type. This can cause a reinterpretation of the bytes of memory.

a.view(ndarray_subclass) or a.view(type=ndarray_subclass) just returns an instance of ndarray_subclass that looks at the same array (same shape, dtype, etc.) This does not cause a reinterpretation of the memory.

For a.view(some_dtype), if some_dtype has a different number of bytes per entry than the previous dtype (for example, converting a regular array to a structured array), then the behavior of the view cannot be predicted just from the superficial appearance of a (shown by print(a)). It also depends on exactly how a is stored in memory. Therefore if a is C-ordered versus fortran-ordered, versus defined as a slice or transpose, etc., the view may give different results.

Examples

>>> x = np.array([(1, 2)], dtype=[('a', np.int8), ('b', np.int8)])

Viewing array data using a different type and dtype:

>>> y = x.view(dtype=np.int16, type=np.matrix)
>>> y
matrix([[513]], dtype=int16)
>>> print(type(y))
<class 'numpy.matrix'>

Creating a view on a structured array so it can be used in calculations

>>> x = np.array([(1, 2),(3,4)], dtype=[('a', np.int8), ('b', np.int8)])
>>> xv = x.view(dtype=np.int8).reshape(-1,2)
>>> xv
array([[1, 2],
       [3, 4]], dtype=int8)
>>> xv.mean(0)
array([2.,  3.])

Making changes to the view changes the underlying array

>>> xv[0,1] = 20
>>> x
array([(1, 20), (3,  4)], dtype=[('a', 'i1'), ('b', 'i1')])

Using a view to convert an array to a recarray:

>>> z = x.view(np.recarray)
>>> z.a
array([1, 3], dtype=int8)

Views share data:

>>> x[0] = (9, 10)
>>> z[0]
(9, 10)

Views that change the dtype size (bytes per entry) should normally be avoided on arrays defined by slices, transposes, fortran-ordering, etc.:

>>> x = np.array([[1,2,3],[4,5,6]], dtype=np.int16)
>>> y = x[:, 0:2]
>>> y
array([[1, 2],
       [4, 5]], dtype=int16)
>>> y.view(dtype=[('width', np.int16), ('length', np.int16)])
Traceback (most recent call last):
    ...
ValueError: To change to a dtype of a different size, the array must be C-contiguous
>>> z = y.copy()
>>> z.view(dtype=[('width', np.int16), ('length', np.int16)])
array([[(1, 2)],
       [(4, 5)]], dtype=[('width', '<i2'), ('length', '<i2')])

whiten(self, fftlength=None, overlap=0, method='welch', window='hanning', detrend='constant', asd=None, fduration=2, highpass=None, **kwargs)[source]¶

Whiten this TimeSeries using inverse spectrum truncation

Parameters

fftlength : float, optional

FFT integration length (in seconds) for ASD estimation, default: choose based on sample rate

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

method : str, optional

FFT-averaging method

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, default: 'hanning' see scipy.signal.get_window() for details on acceptable formats

detrend : str, optional

type of detrending to do before FFT (see detrend for more details), default: 'constant'

asd : FrequencySeries, optional

the amplitude spectral density using which to whiten the data, overrides other ASD arguments, default: None

fduration : float, optional

duration (in seconds) of the time-domain FIR whitening filter, must be no longer than fftlength, default: 2 seconds

highpass : float, optional

highpass corner frequency (in Hz) of the FIR whitening filter, default: None

**kwargs

other keyword arguments are passed to the TimeSeries.asd method to estimate the amplitude spectral density FrequencySeries of this TimeSeries

Returns

out : TimeSeries

a whitened version of the input data with zero mean and unit variance

See also

TimeSeries.asd

for details on the ASD calculation

TimeSeries.convolve

for details on convolution with the overlap-save method

gwpy.signal.filter_design.fir_from_transfer

for FIR filter design through spectrum truncation

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

The window argument is used in ASD estimation, FIR filter design, and in preventing spectral leakage in the output.

Due to filter settle-in, a segment of length 0.5*fduration will be corrupted at the beginning and end of the output. See convolve for more details.

The input is detrended and the output normalised such that, if the input is stationary and Gaussian, then the output will have zero mean and unit variance.

For more on inverse spectrum truncation, see arXiv:gr-qc/0509116.

write(self, target, *args, **kwargs)[source]¶

Write this TimeSeries to a file

Parameters

target : str

path of output file

format : str, optional

output format identifier. If not given, the format will be detected if possible. See below for list of acceptable formats.

Notes

The available built-in formats are:

Format	Read	Write	Auto-identify
csv	Yes	Yes	Yes
gwf	Yes	Yes	Yes
gwf.framecpp	Yes	Yes	No
gwf.lalframe	Yes	Yes	No
hdf5	Yes	Yes	Yes
txt	Yes	Yes	Yes
wav	Yes	Yes	No

zip(self)[source]¶

Zip the xindex and value arrays of this Series

Returns

stacked : 2-d numpy.ndarray

The array formed by stacking the the xindex and value of this series

Examples

>>> a = Series([0, 2, 4, 6, 8], xindex=[-5, -4, -3, -2, -1])
>>> a.zip()
array([[-5.,  0.],
       [-4.,  2.],
       [-3.,  4.],
       [-2.,  6.],
       [-1.,  8.]])

zpk(self, zeros, poles, gain, analog=True, **kwargs)[source]¶

Filter this TimeSeries by applying a zero-pole-gain filter

Parameters

zeros : array-like

list of zero frequencies (in Hertz)

poles : array-like

list of pole frequencies (in Hertz)

gain : float

DC gain of filter

analog : bool, optional

type of ZPK being applied, if analog=True all parameters will be converted in the Z-domain for digital filtering

Returns

timeseries : TimeSeries

the filtered version of the input data

See also

TimeSeries.filter

for details on how a digital ZPK-format filter is applied

Examples

To apply a zpk filter with file poles at 100 Hz, and five zeros at 1 Hz (giving an overall DC gain of 1e-10):

>>> data2 = data.zpk([100]*5, [1]*5, 1e-10)

DictClass[source]¶

alias of TimeSeriesDict

asd(self, fftlength=None, overlap=None, window='hann', method='welch', **kwargs)[source]

Calculate the ASD FrequencySeries of this TimeSeries

Parameters

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

method : str, optional

FFT-averaging method, see Notes for more details

Returns

psd : FrequencySeries

a data series containing the PSD.

See also

TimeSeries.psd

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

auto_coherence(self, dt, fftlength=None, overlap=None, window='hann', **kwargs)[source]

Calculate the frequency-coherence between this TimeSeries and a time-shifted copy of itself.

The standard TimeSeries.coherence() is calculated between the input TimeSeries and a cropped copy of itself. Since the cropped version will be shorter, the input series will be shortened to match.

Parameters

dt : float

duration (in seconds) of time-shift

fftlength : float, optional

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

**kwargs

any other keyword arguments accepted by matplotlib.mlab.cohere() except NFFT, window, and noverlap which are superceded by the above keyword arguments

Returns

coherence : FrequencySeries

the coherence FrequencySeries of this TimeSeries with the other

See also

matplotlib.mlab.cohere

for details of the coherence calculator

Notes

The TimeSeries.auto_coherence() will perform best when dt is approximately fftlength / 2.

average_fft(self, fftlength=None, overlap=0, window=None)[source]

Compute the averaged one-dimensional DFT of this TimeSeries.

This method computes a number of FFTs of duration fftlength and overlap (both given in seconds), and returns the mean average. This method is analogous to the Welch average method for power spectra.

Parameters

fftlength : float

number of seconds in single FFT, default, use whole TimeSeries

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

Returns

out : complex-valued FrequencySeries

the transformed output, with populated frequencies array metadata

See also

TimeSeries.fft

The FFT method used.

bandpass(self, flow, fhigh, gpass=2, gstop=30, fstop=None, type='iir', filtfilt=True, **kwargs)[source]

Filter this TimeSeries with a band-pass filter.

Parameters

flow : float

lower corner frequency of pass band

fhigh : float

upper corner frequency of pass band

gpass : float

the maximum loss in the passband (dB).

gstop : float

the minimum attenuation in the stopband (dB).

fstop : tuple of float, optional

(low, high) edge-frequencies of stop band

type : str

the filter type, either 'iir' or 'fir'

**kwargs

other keyword arguments are passed to gwpy.signal.filter_design.bandpass()

Returns

bpseries : TimeSeries

a band-passed version of the input TimeSeries

See also

gwpy.signal.filter_design.bandpass

for details on the filter design

TimeSeries.filter

for details on how the filter is applied

Notes

When using scipy < 0.16.0 some higher-order filters may be unstable. With scipy >= 0.16.0 higher-order filters are decomposed into second-order-sections, and so are much more stable.

coherence(self, other, fftlength=None, overlap=None, window='hann', **kwargs)[source]

Calculate the frequency-coherence between this TimeSeries and another.

Parameters

other : TimeSeries

TimeSeries signal to calculate coherence with

fftlength : float, optional

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

**kwargs

any other keyword arguments accepted by matplotlib.mlab.cohere() except NFFT, window, and noverlap which are superceded by the above keyword arguments

Returns

coherence : FrequencySeries

the coherence FrequencySeries of this TimeSeries with the other

See also

matplotlib.mlab.cohere

for details of the coherence calculator

Notes

If self and other have difference TimeSeries.sample_rate values, the higher sampled TimeSeries will be down-sampled to match the lower.

coherence_spectrogram(self, other, stride, fftlength=None, overlap=None, window='hann', nproc=1)[source]

Calculate the coherence spectrogram between this TimeSeries and other.

Parameters

other : TimeSeries

the second TimeSeries in this CSD calculation

stride : float

number of seconds in single PSD (column of spectrogram)

fftlength : float

number of seconds in single FFT

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

nproc : int

number of parallel processes to use when calculating individual coherence spectra.

Returns

spectrogram : Spectrogram

time-frequency coherence spectrogram as generated from the input time-series.

convolve(self, fir, window='hanning')[source]

Convolve this TimeSeries with an FIR filter using the

overlap-save method

Parameters

fir : numpy.ndarray

the time domain filter to convolve with

window : str, optional

window function to apply to boundaries, default: 'hanning' see scipy.signal.get_window() for details on acceptable formats

Returns

out : TimeSeries

the result of the convolution

See also

scipy.signal.fftconvolve

for details on the convolution scheme used here

TimeSeries.filter

for an alternative method designed for short filters

Notes

The output TimeSeries is the same length and has the same timestamps as the input.

Due to filter settle-in, a segment half the length of fir will be corrupted at the left and right boundaries. To prevent spectral leakage these segments will be windowed before convolving.

correlate(self, mfilter, window='hanning', detrend='linear', whiten=False, wduration=2, highpass=None, **asd_kw)[source]

Cross-correlate this TimeSeries with another signal

Parameters

mfilter : TimeSeries

the time domain signal to correlate with

window : str, optional

window function to apply to timeseries prior to FFT, default: 'hanning' see scipy.signal.get_window() for details on acceptable formats

detrend : str, optional

type of detrending to do before FFT (see detrend for more details), default: 'linear'

whiten : bool, optional

boolean switch to enable (True) or disable (False) data whitening, default: False

wduration : float, optional

duration (in seconds) of the time-domain FIR whitening filter, only used if whiten=True, defaults to 2 seconds

highpass : float, optional

highpass corner frequency (in Hz) of the FIR whitening filter, only used if whiten=True, default: None

**asd_kw

keyword arguments to pass to TimeSeries.asd to generate an ASD, only used if whiten=True

Returns

snr : TimeSeries

the correlated signal-to-noise ratio (SNR) timeseries

See also

TimeSeries.asd

for details on the ASD calculation

TimeSeries.convolve

for details on convolution with the overlap-save method

Notes

The window argument is used in ASD estimation, whitening, and preventing spectral leakage in the output. It is not used to condition the matched-filter, which should be windowed before passing to this method.

Due to filter settle-in, a segment half the length of mfilter will be corrupted at the beginning and end of the output. See convolve for more details.

The input and matched-filter will be detrended, and the output will be normalised so that the SNR measures number of standard deviations from the expected mean.

csd(self, other, fftlength=None, overlap=None, window='hann', **kwargs)[source]

Calculate the CSD FrequencySeries for two TimeSeries

Parameters

other : TimeSeries

the second TimeSeries in this CSD calculation

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

Returns

csd : FrequencySeries

a data series containing the CSD.

csd_spectrogram(self, other, stride, fftlength=None, overlap=0, window='hann', nproc=1, **kwargs)[source]

Calculate the cross spectral density spectrogram of this

TimeSeries with ‘other’.

Parameters

other : TimeSeries

second time-series for cross spectral density calculation

stride : float

number of seconds in single PSD (column of spectrogram).

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

nproc : int

maximum number of independent frame reading processes, default is set to single-process file reading.

Returns

spectrogram : Spectrogram

time-frequency cross spectrogram as generated from the two input time-series.

demodulate(self, f, stride=1, exp=False, deg=True)[source]

Compute the average magnitude and phase of this TimeSeries once per stride at a given frequency

Parameters

f : float

frequency (Hz) at which to demodulate the signal

stride : float, optional

stride (seconds) between calculations, defaults to 1 second

exp : bool, optional

return the magnitude and phase trends as one TimeSeries object representing a complex exponential, default: False

deg : bool, optional

if exp=False, calculates the phase in degrees

Returns

mag, phase : TimeSeries

if exp=False, returns a pair of TimeSeries objects representing magnitude and phase trends with dt=stride

out : TimeSeries

if exp=True, returns a single TimeSeries with magnitude and phase trends represented as mag * exp(1j*phase) with dt=stride

See also

TimeSeries.heterodyne

for the underlying heterodyne detection method

Examples

Demodulation is useful when trying to examine steady sinusoidal signals we know to be contained within data. For instance, we can download some data from LOSC to look at trends of the amplitude and phase of LIGO Livingston’s calibration line at 331.3 Hz:

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('L1', 1131350417, 1131357617)

We can demodulate the TimeSeries at 331.3 Hz with a stride of one minute:

>>> amp, phase = data.demodulate(331.3, stride=60)

We can then plot these trends to visualize fluctuations in the amplitude of the calibration line:

>>> from gwpy.plot import Plot
>>> plot = Plot(amp)
>>> ax = plot.gca()
>>> ax.set_ylabel('Strain Amplitude at 331.3 Hz')
>>> plot.show()

(png)

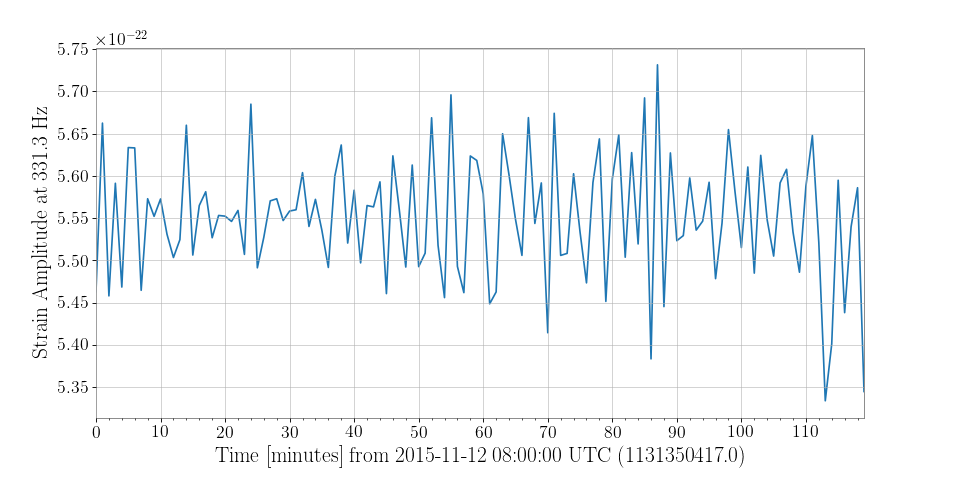
detrend(self, detrend='constant')[source]

Remove the trend from this TimeSeries

This method just wraps scipy.signal.detrend() to return an object of the same type as the input.

Parameters

detrend : str, optional

the type of detrending.

Returns

detrended : TimeSeries

the detrended input series

See also

scipy.signal.detrend

for details on the options for the detrend argument, and how the operation is done

fft(self, nfft=None)[source]

Compute the one-dimensional discrete Fourier transform of this TimeSeries.

Parameters

nfft : int, optional

length of the desired Fourier transform, input will be cropped or padded to match the desired length. If nfft is not given, the length of the TimeSeries will be used

Returns

out : FrequencySeries

the normalised, complex-valued FFT FrequencySeries.

See also

numpy.fft.rfft

The FFT implementation used in this method.

Notes

This method, in constrast to the numpy.fft.rfft() method it calls, applies the necessary normalisation such that the amplitude of the output FrequencySeries is correct.

fftgram(self, fftlength, overlap=None, window='hann', **kwargs)[source]

Calculate the Fourier-gram of this TimeSeries.

At every stride, a single, complex FFT is calculated.

Parameters

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable

Returns

a Fourier-gram

filter(self, *filt, **kwargs)[source]

Filter this TimeSeries with an IIR or FIR filter

Parameters

*filt : filter arguments

1, 2, 3, or 4 arguments defining the filter to be applied,

• an Nx1 ndarray of FIR coefficients

• an Nx6 ndarray of SOS coefficients

• (numerator, denominator) polynomials

• (zeros, poles, gain)

• (A, B, C, D) ‘state-space’ representation

filtfilt : bool, optional

filter forward and backwards to preserve phase, default: False

analog : bool, optional

if True, filter coefficients will be converted from Hz to Z-domain digital representation, default: False

inplace : bool, optional

if True, this array will be overwritten with the filtered version, default: False

**kwargs

other keyword arguments are passed to the filter method

Returns

result : TimeSeries

the filtered version of the input TimeSeries

Raises

ValueError

if filt arguments cannot be interpreted properly

See also

scipy.signal.sosfilt

for details on filtering with second-order sections (scipy >= 0.16 only)

scipy.signal.sosfiltfilt

for details on forward-backward filtering with second-order sections (scipy >= 0.18 only)

scipy.signal.lfilter

for details on filtering (without SOS)

scipy.signal.filtfilt

for details on forward-backward filtering (without SOS)

Notes

IIR filters are converted either into cascading second-order sections (if scipy >= 0.16 is installed), or into the (numerator, denominator) representation before being applied to this TimeSeries.

When using scipy < 0.16 some higher-order filters may be unstable. With scipy >= 0.16 higher-order filters are decomposed into second-order-sections, and so are much more stable.

FIR filters are passed directly to scipy.signal.lfilter() or scipy.signal.filtfilt() without any conversions.

Examples

We can design an arbitrarily complicated filter using gwpy.signal.filter_design

>>> from gwpy.signal import filter_design
>>> bp = filter_design.bandpass(50, 250, 4096.)
>>> notches = [filter_design.notch(f, 4096.) for f in (60, 120, 180)]
>>> zpk = filter_design.concatenate_zpks(bp, *notches)

And then can download some data from LOSC to apply it using TimeSeries.filter:

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('H1', 1126259446, 1126259478)
>>> filtered = data.filter(zpk, filtfilt=True)

We can plot the original signal, and the filtered version, cutting off either end of the filtered data to remove filter-edge artefacts

>>> from gwpy.plot import Plot
>>> plot = Plot(data, filtered[128:-128], separate=True)
>>> plot.show()

(png)

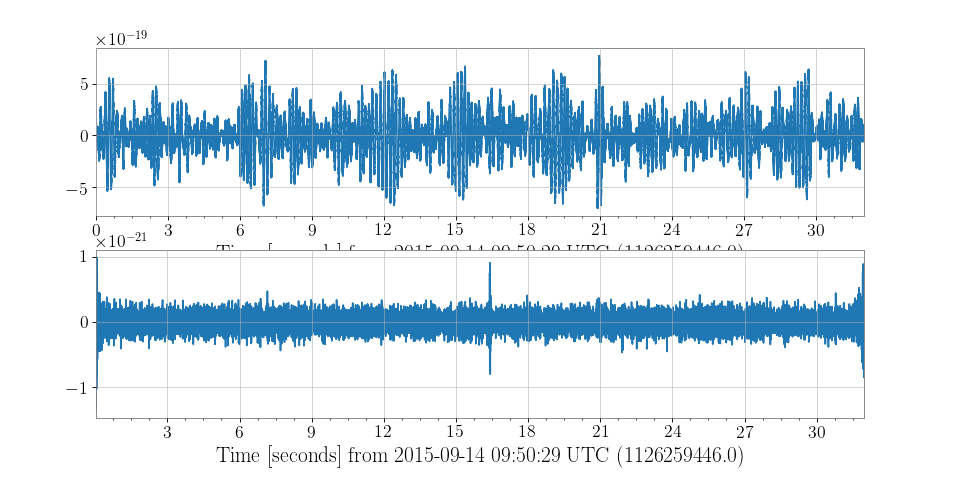
gate(self, tzero=1.0, tpad=0.5, whiten=True, threshold=50.0, cluster_window=0.5, **whiten_kwargs)[source]

Removes high amplitude peaks from data using inverse Planck window.

Points will be discovered automatically using a provided threshold and clustered within a provided time window.

Parameters

tzero : int, optional

half-width time duration in which the time series is set to zero

tpad : int, optional

half-width time duration in which the Planck window is tapered

whiten : bool, optional

if True, data will be whitened before gating points are discovered, use of this option is highly recommended

threshold : float, optional

amplitude threshold, if the data exceeds this value a gating window will be placed

cluster_window : float, optional

time duration over which gating points will be clustered

**whiten_kwargs

other keyword arguments that will be passed to the TimeSeries.whiten method if it is being used when discovering gating points

Returns

out : TimeSeries

a copy of the original TimeSeries that has had gating windows applied

Examples

Read data into a TimeSeries

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('H1', 1135148571, 1135148771)

Apply gating using custom arguments

>>> gated = data.gate(tzero=1.0, tpad=1.0, threshold=10.0,
                      fftlength=4, overlap=2, method='median')

Plot the original data and the gated data, whiten both for visualization purposes

>>> overlay = data.whiten(4,2,method='median').plot(dpi=150,
                          label='Ungated', color='dodgerblue',
                          zorder=2)
>>> ax = overlay.gca()
>>> ax.plot(gated.whiten(4,2,method='median'), label='Gated',
            color='orange', zorder=3)
>>> ax.set_xlim(1135148661, 1135148681)
>>> ax.legend()
>>> overlay.show()

heterodyne(self, phase, stride=1, singlesided=False)[source]

Compute the average magnitude and phase of this TimeSeries once per stride after heterodyning with a given phase series

Parameters

phase : array_like

an array of phase measurements (radians) with which to heterodyne the signal

stride : float, optional

stride (seconds) between calculations, defaults to 1 second

singlesided : bool, optional

Boolean switch to return single-sided output (i.e., to multiply by 2 so that the signal is distributed across positive frequencies only), default: False

Returns

out : TimeSeries

magnitude and phase trends, represented as mag * exp(1j*phase) with dt=stride

See also

TimeSeries.demodulate

for a method to heterodyne at a fixed frequency

Notes

This is similar to the demodulate() method, but is more general in that it accepts a varying phase evolution, rather than a fixed frequency.

Unlike demodulate(), the complex output is double-sided by default, so is not multiplied by 2.

Examples

Heterodyning can be useful in analysing quasi-monochromatic signals with a known phase evolution, such as continuous-wave signals from rapidly rotating neutron stars. These sources radiate at a frequency that slowly decreases over time, and is Doppler modulated due to the Earth’s rotational and orbital motion.

To see an example of heterodyning in action, we can simulate a signal whose phase evolution is described by the frequency and its first derivative with respect to time. We can download some O1 era LIGO-Livingston data from GWOSC, inject the simulated signal, and recover its amplitude.

>>> from gwpy.timeseries import TimeSeries
>>> data = TimeSeries.fetch_open_data('L1', 1131350417, 1131354017)

We now need to set the signal parameters, generate the expected phase evolution, and create the signal:

>>> import numpy
>>> f0 = 123.456789  # signal frequency (Hz)
>>> fdot = -9.87654321e-7  # signal frequency derivative (Hz/s)
>>> fpeoch = 1131350417  # phase epoch
>>> amp = 1.5e-22  # signal amplitude
>>> phase0 = 0.4  # signal phase at the phase epoch
>>> times = data.times.value - fepoch
>>> phase = 2 * numpy.pi * (f0 * times + 0.5 * fdot * times**2)
>>> signal = TimeSeries(amp * numpy.cos(phase + phase0),
>>>                     sample_rate=data.sample_rate, t0=data.t0)
>>> data = data.inject(signal)

To recover the signal, we can bandpass the injected data around the signal frequency, then heterodyne using our phase model with a stride of 60 seconds:

>>> filtdata = data.bandpass(f0 - 0.5, f0 + 0.5)
>>> het = filtdata.heterodyne(phase, stride=60, singlesided=True)

We can then plot signal amplitude over time (cropping the first two minutes to remove the filter response):

>>> plot = het.crop(het.x0.value + 180).abs().plot()
>>> ax = plot.gca()
>>> ax.set_ylabel("Strain amplitude")
>>> plot.show()

highpass(self, frequency, gpass=2, gstop=30, fstop=None, type='iir', filtfilt=True, **kwargs)[source]

Filter this TimeSeries with a high-pass filter.

Parameters

frequency : float

high-pass corner frequency

gpass : float

the maximum loss in the passband (dB).

gstop : float

the minimum attenuation in the stopband (dB).

fstop : float

stop-band edge frequency, defaults to frequency * 1.5

type : str

the filter type, either 'iir' or 'fir'

**kwargs

other keyword arguments are passed to gwpy.signal.filter_design.highpass()

Returns

hpseries : TimeSeries

a high-passed version of the input TimeSeries

See also

gwpy.signal.filter_design.highpass

for details on the filter design

TimeSeries.filter

for details on how the filter is applied

Notes

When using scipy < 0.16.0 some higher-order filters may be unstable. With scipy >= 0.16.0 higher-order filters are decomposed into second-order-sections, and so are much more stable.

lowpass(self, frequency, gpass=2, gstop=30, fstop=None, type='iir', filtfilt=True, **kwargs)[source]

Filter this TimeSeries with a Butterworth low-pass filter.

Parameters

frequency : float

low-pass corner frequency

gpass : float

the maximum loss in the passband (dB).

gstop : float

the minimum attenuation in the stopband (dB).

fstop : float

stop-band edge frequency, defaults to frequency * 1.5

type : str

the filter type, either 'iir' or 'fir'

**kwargs

other keyword arguments are passed to gwpy.signal.filter_design.lowpass()

Returns

lpseries : TimeSeries

a low-passed version of the input TimeSeries

See also

gwpy.signal.filter_design.lowpass

for details on the filter design

TimeSeries.filter

for details on how the filter is applied

Notes

When using scipy < 0.16.0 some higher-order filters may be unstable. With scipy >= 0.16.0 higher-order filters are decomposed into second-order-sections, and so are much more stable.

notch(self, frequency, type='iir', filtfilt=True, **kwargs)[source]

Notch out a frequency in this TimeSeries.

Parameters

frequency : float, Quantity

frequency (default in Hertz) at which to apply the notch

type : str, optional

type of filter to apply, currently only ‘iir’ is supported

**kwargs

other keyword arguments to pass to scipy.signal.iirdesign

Returns

notched : TimeSeries

a notch-filtered copy of the input TimeSeries

See also

TimeSeries.filter

for details on the filtering method

scipy.signal.iirdesign

for details on the IIR filter design method

psd(self, fftlength=None, overlap=None, window='hann', method='welch', **kwargs)[source]

Calculate the PSD FrequencySeries for this TimeSeries

Parameters

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

method : str, optional

FFT-averaging method, see Notes for more details

**kwargs

other keyword arguments are passed to the underlying PSD-generation method

Returns

psd : FrequencySeries

a data series containing the PSD.

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

q_gram(self, qrange=(4, 64), frange=(0, inf), mismatch=0.2, snrthresh=5.5, **kwargs)[source]

Scan a TimeSeries using the multi-Q transform and return an EventTable of the most significant tiles

Parameters

qrange : tuple of float, optional

(low, high) range of Qs to scan

frange : tuple of float, optional

(low, high) range of frequencies to scan

mismatch : float, optional

maximum allowed fractional mismatch between neighbouring tiles

snrthresh : float, optional

lower inclusive threshold on individual tile SNR to keep in the table

**kwargs

other keyword arguments to be passed to QTiling.transform(), including 'epoch' and 'search'

Returns

qgram : EventTable

a table of time-frequency tiles on the most significant QPlane

See also

TimeSeries.q_transform

for a method to interpolate the raw Q-transform over a regularly gridded spectrogram

gwpy.signal.qtransform

for code and documentation on how the Q-transform is implemented

gwpy.table.EventTable.tile

to render this EventTable as a collection of polygons

Notes

Only tiles with signal energy greater than or equal to snrthresh ** 2 / 2 will be stored in the output EventTable. The table columns are 'time', 'duration', 'frequency', 'bandwidth', and 'energy'.

q_transform(self, qrange=(4, 64), frange=(0, inf), gps=None, search=0.5, tres='<default>', fres='<default>', logf=False, norm='median', mismatch=0.2, outseg=None, whiten=True, fduration=2, highpass=None, **asd_kw)[source]

Scan a TimeSeries using the multi-Q transform and return an interpolated high-resolution spectrogram

By default, this method returns a high-resolution spectrogram in both time and frequency, which can result in a large memory footprint. If you know that you only need a subset of the output for, say, a figure, consider using outseg and the other keyword arguments to restrict the size of the returned data.

Parameters

qrange : tuple of float, optional

(low, high) range of Qs to scan

frange : tuple of float, optional

(log, high) range of frequencies to scan

gps : float, optional

central time of interest for determine loudest Q-plane

search : float, optional

window around gps in which to find peak energies, only used if gps is given

tres : float, optional

desired time resolution (seconds) of output Spectrogram, default is abs(outseg) / 1000.

fres : float, int, None, optional

desired frequency resolution (Hertz) of output Spectrogram, or, if logf=True, the number of frequency samples; give None to skip this step and return the original resolution, default is 0.5 Hz or 500 frequency samples

logf : bool, optional

boolean switch to enable (True) or disable (False) use of log-sampled frequencies in the output Spectrogram, if True then fres is interpreted as a number of frequency samples, default: False

norm : bool, str, optional

whether to normalize the returned Q-transform output, or how, default: True ('median'), other options: False, 'mean'

mismatch : float

maximum allowed fractional mismatch between neighbouring tiles

outseg : Segment, optional

GPS [start, stop) segment for output Spectrogram, default is the full duration of the input

whiten : bool, FrequencySeries, optional

boolean switch to enable (True) or disable (False) data whitening, or an ASD FrequencySeries with which to whiten the data

fduration : float, optional

duration (in seconds) of the time-domain FIR whitening filter, only used if whiten is not False, defaults to 2 seconds

highpass : float, optional

highpass corner frequency (in Hz) of the FIR whitening filter, used only if whiten is not False, default: None

**asd_kw

keyword arguments to pass to TimeSeries.asd to generate an ASD to use when whitening the data

Returns

out : Spectrogram

output Spectrogram of normalised Q energy

See also

TimeSeries.asd

for documentation on acceptable **asd_kw

TimeSeries.whiten

for documentation on how the whitening is done

gwpy.signal.qtransform

for code and documentation on how the Q-transform is implemented

Notes

This method will return a Spectrogram of dtype float32 if norm is given, and float64 otherwise.

To optimize plot rendering with pcolormesh, the output Spectrogram can be given a log-sampled frequency axis by passing logf=True at runtime. The fres argument is then the number of points on the frequency axis. Note, this is incompatible with imshow.

It is also highly recommended to use the outseg keyword argument when only a small window around a given GPS time is of interest. This will speed up this method a little, but can greatly speed up rendering the resulting Spectrogram using pcolormesh.

If you aren’t going to use pcolormesh in the end, don’t worry.

Examples

>>> from numpy.random import normal
>>> from scipy.signal import gausspulse
>>> from gwpy.timeseries import TimeSeries

Generate a TimeSeries containing Gaussian noise sampled at 4096 Hz, centred on GPS time 0, with a sine-Gaussian pulse (‘glitch’) at 500 Hz:

>>> noise = TimeSeries(normal(loc=1, size=4096*4), sample_rate=4096, epoch=-2)
>>> glitch = TimeSeries(gausspulse(noise.times.value, fc=500) * 4, sample_rate=4096)
>>> data = noise + glitch

Compute and plot the Q-transform of these data:

>>> q = data.q_transform()
>>> plot = q.plot()
>>> ax = plot.gca()
>>> ax.set_xlim(-.2, .2)
>>> ax.set_epoch(0)
>>> plot.show()

(png)

rayleigh_spectrogram(self, stride, fftlength=None, overlap=0, nproc=1, **kwargs)[source]

Calculate the Rayleigh statistic spectrogram of this TimeSeries

Parameters

stride : float

number of seconds in single PSD (column of spectrogram).

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, default: 0

nproc : int, optional

maximum number of independent frame reading processes, default default: 1

Returns

spectrogram : Spectrogram

time-frequency Rayleigh spectrogram as generated from the input time-series.

See also

TimeSeries.rayleigh

for details of the statistic calculation

rayleigh_spectrum(self, fftlength=None, overlap=None)[source]

Calculate the Rayleigh FrequencySeries for this TimeSeries.

The Rayleigh statistic is calculated as the ratio of the standard deviation and the mean of a number of periodograms.

Parameters

fftlength : float

number of seconds in single FFT, defaults to a single FFT covering the full duration

overlap : float, optional

number of seconds of overlap between FFTs, defaults to that of the relevant method.

Returns

psd : FrequencySeries

a data series containing the PSD.

resample(self, rate, window='hamming', ftype='fir', n=None)[source]

Resample this Series to a new rate

Parameters

rate : float

rate to which to resample this Series

window : str, numpy.ndarray, optional

window function to apply to signal in the Fourier domain, see scipy.signal.get_window() for details on acceptable formats, only used for ftype='fir' or irregular downsampling

ftype : str, optional

type of filter, either ‘fir’ or ‘iir’, defaults to ‘fir’

n : int, optional

if ftype='fir' the number of taps in the filter, otherwise the order of the Chebyshev type I IIR filter

Returns

Series

a new Series with the resampling applied, and the same metadata

rms(self, stride=1)[source]

Calculate the root-mean-square value of this TimeSeries once per stride.

Parameters

stride : float

stride (seconds) between RMS calculations

Returns

rms : TimeSeries

a new TimeSeries containing the RMS value with dt=stride

spectral_variance(self, stride, fftlength=None, overlap=None, method='welch', window='hann', nproc=1, filter=None, bins=None, low=None, high=None, nbins=500, log=False, norm=False, density=False)[source]

Calculate the SpectralVariance of this TimeSeries.

Parameters

stride : float

number of seconds in single PSD (column of spectrogram)

fftlength : float

number of seconds in single FFT

method : str, optional

FFT-averaging method, see Notes for more details

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

nproc : int

maximum number of independent frame reading processes, default is set to single-process file reading.

bins : numpy.ndarray, optional, default None

array of histogram bin edges, including the rightmost edge

low : float, optional

left edge of lowest amplitude bin, only read if bins is not given

high : float, optional

right edge of highest amplitude bin, only read if bins is not given

nbins : int, optional

number of bins to generate, only read if bins is not given

log : bool, optional

calculate amplitude bins over a logarithmic scale, only read if bins is not given

norm : bool, optional

normalise bin counts to a unit sum

density : bool, optional

normalise bin counts to a unit integral

Returns

specvar : SpectralVariance

2D-array of spectral frequency-amplitude counts

See also

numpy.histogram

for details on specifying bins and weights

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

spectrogram(self, stride, fftlength=None, overlap=None, window='hann', method='welch', nproc=1, **kwargs)[source]

Calculate the average power spectrogram of this TimeSeries using the specified average spectrum method.

Each time-bin of the output Spectrogram is calculated by taking a chunk of the TimeSeries in the segment [t - overlap/2., t + stride + overlap/2.) and calculating the psd() of those data.

As a result, each time-bin is calculated using stride + overlap seconds of data.

Parameters

stride : float

number of seconds in single PSD (column of spectrogram).

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

method : str, optional

FFT-averaging method, see Notes for more details

nproc : int

number of CPUs to use in parallel processing of FFTs

Returns

spectrogram : Spectrogram

time-frequency power spectrogram as generated from the input time-series.

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

spectrogram2(self, fftlength, overlap=None, window='hann', **kwargs)[source]

Calculate the non-averaged power Spectrogram of this TimeSeries

Parameters

fftlength : float

number of seconds in single FFT.

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, see scipy.signal.get_window() for details on acceptable formats

scaling : [ ‘density’ | ‘spectrum’ ], optional

selects between computing the power spectral density (‘density’) where the Spectrogram has units of V**2/Hz if the input is measured in V and computing the power spectrum (‘spectrum’) where the Spectrogram has units of V**2 if the input is measured in V. Defaults to ‘density’.

**kwargs

other parameters to be passed to scipy.signal.periodogram for each column of the Spectrogram

Returns

spectrogram: Spectrogram

a power Spectrogram with 1/fftlength frequency resolution and (fftlength - overlap) time resolution.

See also

scipy.signal.periodogram

for documentation on the Fourier methods used in this calculation

Notes

This method calculates overlapping periodograms for all possible chunks of data entirely containing within the span of the input TimeSeries, then normalises the power in overlapping chunks using a triangular window centred on that chunk which most overlaps the given Spectrogram time sample.

taper(self, side='leftright', duration=None, nsamples=None)[source]

Taper the ends of this TimeSeries smoothly to zero.

Parameters

side : str, optional

the side of the TimeSeries to taper, must be one of 'left', 'right', or 'leftright'

duration : float, optional

the duration of time to taper, will override nsamples if both are provided as arguments

nsamples : int, optional

the number of samples to taper, will be overridden by duration if both are provided as arguments

Returns

out : TimeSeries

a copy of self tapered at one or both ends

Raises

ValueError

if side is not one of ('left', 'right', 'leftright')

Notes

The TimeSeries.taper() automatically tapers from the second stationary point (local maximum or minimum) on the specified side of the input. However, the method will never taper more than half the full width of the TimeSeries, and will fail if there are no stationary points.

See planck() for the generic Planck taper window, and see scipy.signal.get_window() for other common window formats.

Examples

To see the effect of the Planck-taper window, we can taper a sinusoidal TimeSeries at both ends:

>>> import numpy
>>> from gwpy.timeseries import TimeSeries
>>> t = numpy.linspace(0, 1, 2048)
>>> series = TimeSeries(numpy.cos(10.5*numpy.pi*t), times=t)
>>> tapered = series.taper()

We can plot it to see how the ends now vary smoothly from 0 to 1:

>>> from gwpy.plot import Plot
>>> plot = Plot(series, tapered, separate=True, sharex=True)
>>> plot.show()

(png)

whiten(self, fftlength=None, overlap=0, method='welch', window='hanning', detrend='constant', asd=None, fduration=2, highpass=None, **kwargs)[source]

Whiten this TimeSeries using inverse spectrum truncation

Parameters

fftlength : float, optional

FFT integration length (in seconds) for ASD estimation, default: choose based on sample rate

overlap : float, optional

number of seconds of overlap between FFTs, defaults to the recommended overlap for the given window (if given), or 0

method : str, optional

FFT-averaging method

window : str, numpy.ndarray, optional

window function to apply to timeseries prior to FFT, default: 'hanning' see scipy.signal.get_window() for details on acceptable formats

detrend : str, optional

type of detrending to do before FFT (see detrend for more details), default: 'constant'

asd : FrequencySeries, optional

the amplitude spectral density using which to whiten the data, overrides other ASD arguments, default: None

fduration : float, optional

duration (in seconds) of the time-domain FIR whitening filter, must be no longer than fftlength, default: 2 seconds

highpass : float, optional

highpass corner frequency (in Hz) of the FIR whitening filter, default: None

**kwargs

other keyword arguments are passed to the TimeSeries.asd method to estimate the amplitude spectral density FrequencySeries of this TimeSeries

Returns

out : TimeSeries

a whitened version of the input data with zero mean and unit variance

See also

TimeSeries.asd

for details on the ASD calculation

TimeSeries.convolve

for details on convolution with the overlap-save method

gwpy.signal.filter_design.fir_from_transfer

for FIR filter design through spectrum truncation

Notes

The accepted method arguments are:

• 'bartlett' : a mean average of non-overlapping periodograms

• 'median' : a median average of overlapping periodograms

• 'welch' : a mean average of overlapping periodograms

The window argument is used in ASD estimation, FIR filter design, and in preventing spectral leakage in the output.

Due to filter settle-in, a segment of length 0.5*fduration will be corrupted at the beginning and end of the output. See convolve for more details.

The input is detrended and the output normalised such that, if the input is stationary and Gaussian, then the output will have zero mean and unit variance.

For more on inverse spectrum truncation, see arXiv:gr-qc/0509116.

zpk(self, zeros, poles, gain, analog=True, **kwargs)[source]

Filter this TimeSeries by applying a zero-pole-gain filter

Parameters

zeros : array-like

list of zero frequencies (in Hertz)

poles : array-like

list of pole frequencies (in Hertz)

gain : float

DC gain of filter

analog : bool, optional

type of ZPK being applied, if analog=True all parameters will be converted in the Z-domain for digital filtering

Returns

timeseries : TimeSeries

the filtered version of the input data

See also

TimeSeries.filter

for details on how a digital ZPK-format filter is applied

Examples

To apply a zpk filter with file poles at 100 Hz, and five zeros at 1 Hz (giving an overall DC gain of 1e-10):

>>> data2 = data.zpk([100]*5, [1]*5, 1e-10)