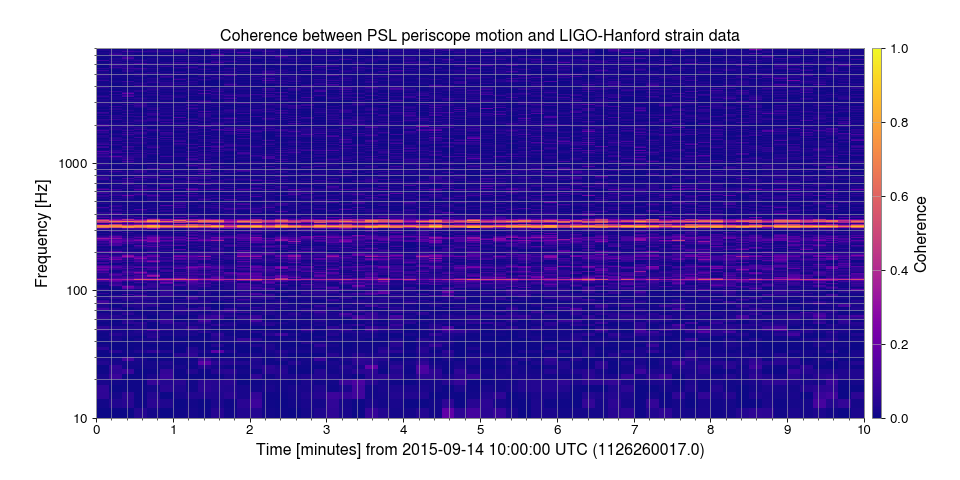
4. Calculating the time-dependent coherence between two channels¶

The standard coherence calculation outputs a frequency series (FrequencySeries) giving a time-averaged measure of coherence. See Calculating the coherence between two channels for an example.

The TimeSeries method coherence_spectrogram() performs the same coherence calculation every stride, giving a time-varying coherence measure.

First, we import the TimeSeriesDict

from gwpy.timeseries import TimeSeriesDict

and then get() the data for the strain output (H1:GDS-CALIB_STRAIN) and the PSL periscope accelerometer (H1:PEM-CS_ACC_PSL_PERISCOPE_X_DQ):

data = TimeSeriesDict.get(
    ['H1:GDS-CALIB_STRAIN', 'H1:PEM-CS_ACC_PSL_PERISCOPE_X_DQ'],
    1126260017,
    1126260617,
)
hoft = data['H1:GDS-CALIB_STRAIN']
acc = data['H1:PEM-CS_ACC_PSL_PERISCOPE_X_DQ']

We can then calculate the coherence() of one TimeSeries with respect to the other, using an 2-second Fourier transform length, with a 1-second (50%) overlap:

coh = hoft.coherence_spectrogram(acc, 10, fftlength=.5, overlap=.25)

Finally, we can plot() the resulting data

plot = coh.plot()
ax = plot.gca()
ax.set_ylabel('Frequency [Hz]')
ax.set_yscale('log')
ax.set_ylim(10, 8000)
ax.set_title(
    'Coherence between PSL periscope motion and LIGO-Hanford strain data',
)
ax.grid(True, 'both', 'both')
ax.colorbar(label='Coherence', clim=[0, 1], cmap='plasma')
plot.show()

(png)